IPv6 Exhaustion Counter Calculation

Rate of Consumption

(Zero on April 1, 2011) and (1% on Jan 1, 2013)

(Click image for full-size)

Eyeballing Google's chart here:

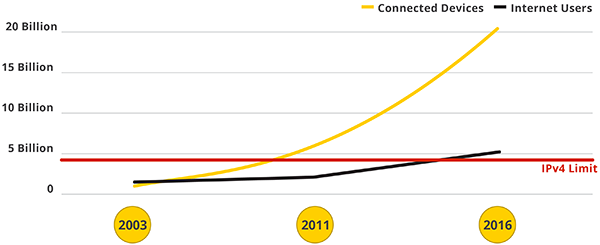
There are about 8 billion devices on the Internet now.

Ignoring all other information & corrections, I just multiplied those numbers together to make a really crude & inaccurate estimate of IPv6 growth:

1% of 8 billion in 1.75 yrs = 80 million per 1.75 yrs = 45 million per year

1 year has 31.5 million seconds.

So the current address consumption rate is approximately 2 per second (rounded up from 1.5 per second to make a conservative estimate).

Projected Exhaustion Date

April 1, 2011 + 2^128 addresses / (2 addresses per second)

1 year = 31536000 seconds

2^127 seconds = 1.7014118 x 10^38 seconds = 170141180 x 10^30 seconds

= ( 170141180 / 31536000 ) x 10^30 years

= 5.395 x 10^30 years

= The year 5,395,000,000,000,000,000,000,000,000,000 AD

Adding 2011 is insignificant.

Another Calculation

@paulgear1: @tbourke @ecbanks @sambowne The number of IPv6 addresses is irrelevant; the number of /64s is what's significant. How does that counter go?

Not all companies get the same size blocks, either. Originally each company was supposed to get a /48, but now some companies get smaller blocks like /56 or even smaller, and some get larger blocks.

Here's some data from Wikipedia:

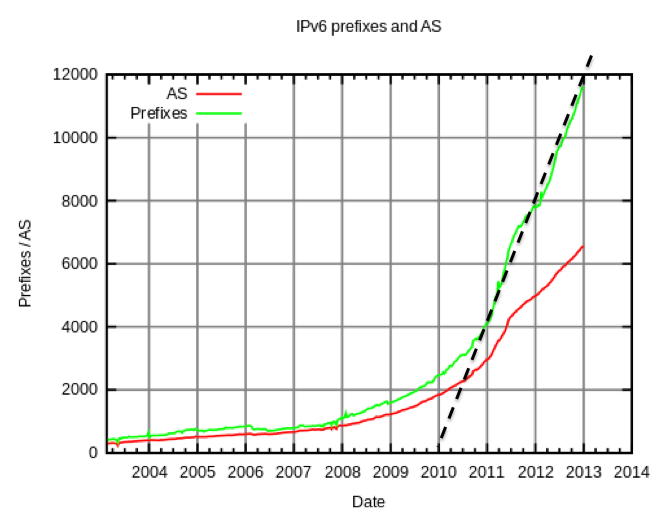
I drew a line projecting current growth, connecting these two points:

(Zero on Jan 1, 2010) and (12,000 on Jan 1, 2013)

So the projected exhaustion date depends on how large those prefixes are.

Here's a chart showing my estimates of the lower and higher bound of reasonable prefix estimates.

Prefix Size       Number of Prefixes            Exhaustion Date
-----------    -----------------------       ------------------------
    /32                  4.295 billion                   1,076,000 AD
    /48                281,500 billion              70,370,000,000 AD
    /64         18,450,000,000 billion       4,611,000,000,000,000 AD

4000 /48 prefixes allocated per year =
4000 / (3.15 x 10^7) prefixes per second = 1.3 x 10-4 prefixes per second

Rounded up: 0.0002 prefixes per second

Sources

http://www.google.com/ipv6/index.html

http://en.wikipedia.org/wiki/IPv6_deployment

http://www.rune-server.org/programming/website-development/220502-creating-auto-updating-clock.html

http://stackoverflow.com/questions/2901102/how-to-print-a-number-with-commas-as-thousands-separators-in-javascript