ML 180: Fitting Polynomials to Data (15 pts + 15 extra)

What You Need

Purpose

To learn the fundamentals of least-square fitting polynomials to data.

This is an old, classic, method which doesn't need neural networks. However, as you will see, it often produces poor results, especially if the power is too high.

Using Google Colab

In a browser, go to
https://colab.research.google.com/
If you see a blue "Sign In" button at the top right, click it and log into a Google account.

From the menu, click File, "New notebook".

Fitting Simple Data

We'll start with data that follows a parabola (degree 2), plus noise.

Execute this code: 

import numpy as np
import matplotlib.pyplot as plt

# Specify seed to make random numbers reproducible
np.random.seed(0)

# Generate some noisy data
x = np.linspace(0, 10, 20)
y = 2 * x**2 + 3 * x + 1 + np.random.normal(0, 10, 20)

degree = 2

# Fit a polynomial
coeffs, res, _, _, _ = np.polyfit(x, y, degree, full=True)

# Create a polynomial function using the coefficients
poly_func = np.poly1d(coeffs)

# Generate y values for the fitted curve
y_fit = poly_func(x)

# Plot the original data and the fitted curve
plt.scatter(x, y, label="Data")
plt.plot(x, y_fit, label="Fitted Curve", color="red")

plt.title("Polynomial of degree "+ str(degree) + \
          " Residuals: " + str(round(res[0], 2)))
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.show()
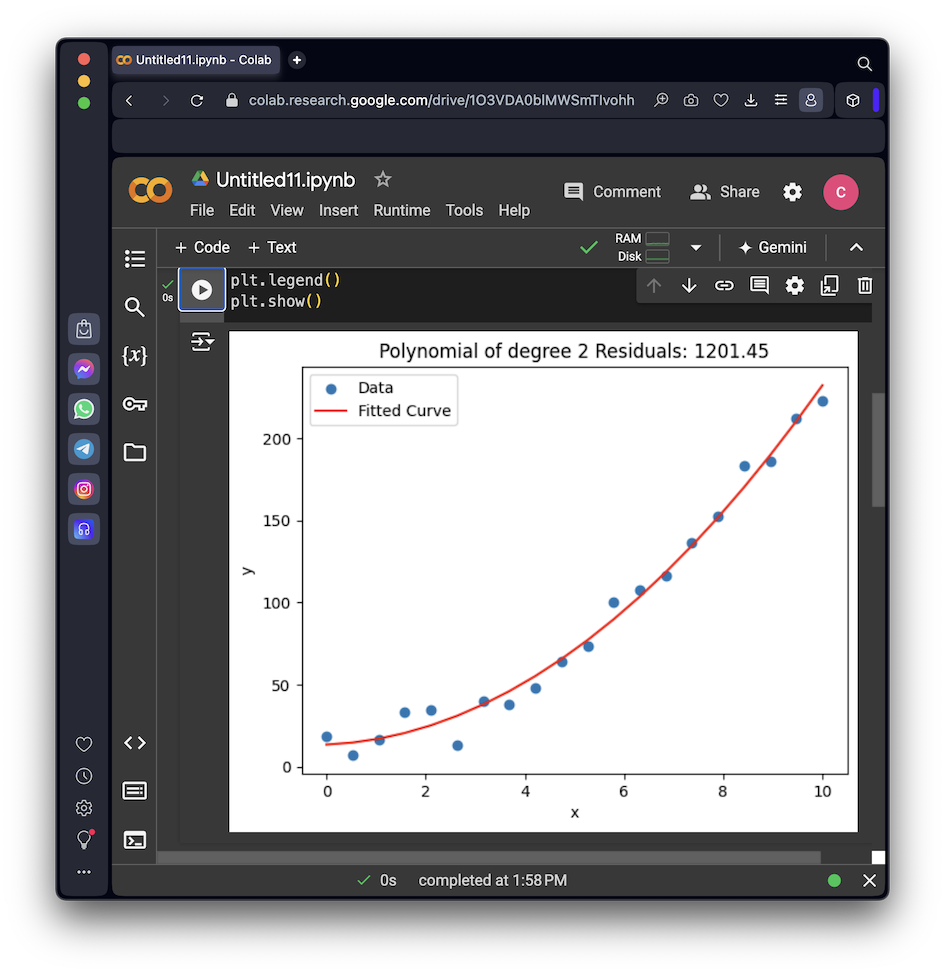
As shown below, the curve is a good fit to the data. This is expected, since the data is in fact close to a parabola, a polynomial of degree 2.

Notice the "Residuals" value--this is the sum of the squared errors. The lower this value, the better the fit to the data.

Degree Too Low

Change the code above to use degree==1 (a line).

As shown below, it fits the best line possible through the data, but it has systematic errors: the dots are all below the line in the middle, and above it at the ends. This is unavoidable because the dots follow a curved parabola, so no straight line can model that behavior.

Notice that the Residuals is much larger, indicating that this is an inferior fit to the data.

Degree Too High

Change the code above to use degree==3.

As shown below, the fit still looks good, and the Residuals are lower than the fit with degree=2. But we know the underlying trend is a parabola, so the 3rd-order term must be fitting the noise, not the trend.

To detect this problem, we'd need a separate set of test data to evaluate the fit, with the same trend but different noise.

ML 180.1: Degree Nine (5 pts)

Change the code above to use degree==9.

As shown below, the fit follows the noise more closely.

The flag is covered by a green rectangle in the image below.

ML 180.2: Fewer Points (10 pts)

In the code above, this line creates a list of X values going from 0 to 10, with a total of 20 points: 
x = np.linspace(0, 10, 20)
Change that line to this line, which produces only 10 points: 
x = np.linspace(0, 10, 19)
You will also need to change this line using 
np.random.normal(0, 10, 20)
to: 
np.random.normal(0, 10, 10)
Now add a new list named x_plot which has 50 points, and use it to plot the predicted curve.

Fit the data with degree=8.

The flag is covered by a green rectangle in the image below.

ML 180.3: Complex Curve (15 pts)

Instead of a parabola, use this data, which produces 100 points on a complex curve: 
y = x*np.cos(2*x) + 0.1*np.random.normal(0, 10, 100)
Fit a 15th degree polynomial.

The flag is covered by a green rectangle in the image below.

Posted 5-21-24
Tip to enable inline suggestions added 7-24-24