ML 116: k-Means Clustering (30 pts extra)

What You Need

Purpose

To practice implementing Random Forests.

Using Google Colab

In a browser, go to
https://colab.research.google.com/
If you see a blue "Sign In" button at the top right, click it and log into a Google account.

From the menu, click File, "New notebook".

Installing Scikit-Learn

You need to use this specific version to get the flags correct.

Execute this command: 

!pip install -v "scikit-learn==1.2.2"
Restart the runtime when you are prompted to.

Making a Dataset

Execute these commands make a dataset with points in five clusters: 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

# extra code – the exact arguments of make_blobs() are not important
blob_centers = np.array([[ 0.2,  2.3], [-1.5 ,  2.3], [-2.8,  1.8],
                         [-2.8,  2.8], [-2.8,  1.3]])
blob_std = np.array([0.4, 0.3, 0.1, 0.1, 0.1])
X, y = make_blobs(n_samples=2000, centers=blob_centers, cluster_std=blob_std,
                  random_state=7)

def plot_clusters(X, y=None):
    plt.scatter(X[:, 0], X[:, 1], c=y, s=1)
    plt.xlabel("$x_1$")
    plt.ylabel("$x_2$", rotation=0)

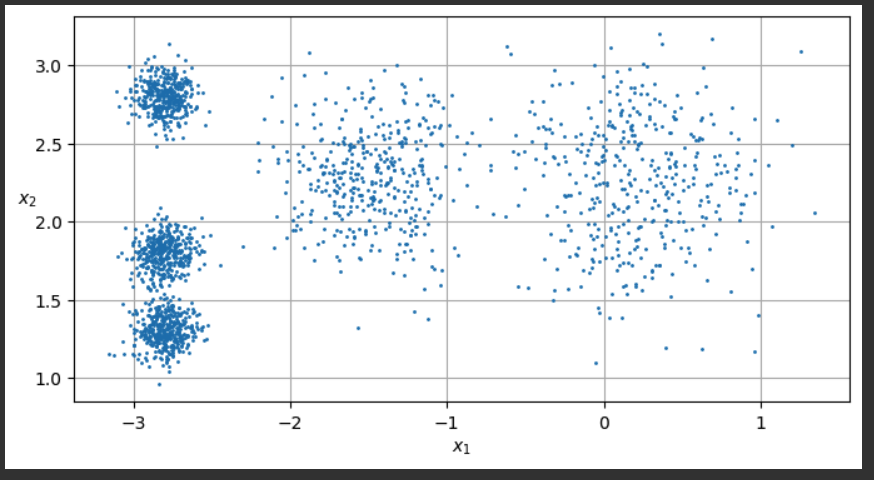
plt.figure(figsize=(8, 4))
plot_clusters(X)
plt.gca().set_axisbelow(True)
plt.grid()
plt.show()
As shown below, the points are in five clusters, of two different sizes.

Fitting a k-Means Model

Execute these commands make fit a k-Means model to the data: 
from sklearn.cluster import KMeans

k = 5
kmeans = KMeans(n_clusters=k, random_state=42, n_init=10)
y_pred = kmeans.fit_predict(X)

def plot_data(X):
    plt.plot(X[:, 0], X[:, 1], 'k.', markersize=2)

def plot_centroids(centroids, weights=None, circle_color='w', cross_color='k'):
    if weights is not None:
        centroids = centroids[weights > weights.max() / 10]
    plt.scatter(centroids[:, 0], centroids[:, 1],
                marker='o', s=35, linewidths=8,
                color=circle_color, zorder=10, alpha=0.9)
    plt.scatter(centroids[:, 0], centroids[:, 1],
                marker='x', s=2, linewidths=12,
                color=cross_color, zorder=11, alpha=1)

def plot_decision_boundaries(clusterer, X, resolution=1000, show_centroids=True,
                             show_xlabels=True, show_ylabels=True):
    mins = X.min(axis=0) - 0.1
    maxs = X.max(axis=0) + 0.1
    xx, yy = np.meshgrid(np.linspace(mins[0], maxs[0], resolution),
                         np.linspace(mins[1], maxs[1], resolution))
    Z = clusterer.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    plt.contourf(Z, extent=(mins[0], maxs[0], mins[1], maxs[1]),
                cmap="Pastel2")
    plt.contour(Z, extent=(mins[0], maxs[0], mins[1], maxs[1]),
                linewidths=1, colors='k')
    plot_data(X)
    if show_centroids:
        plot_centroids(clusterer.cluster_centers_)

    if show_xlabels:
        plt.xlabel("$x_1$")
    else:
        plt.tick_params(labelbottom=False)
    if show_ylabels:
        plt.ylabel("$x_2$", rotation=0)
    else:
        plt.tick_params(labelleft=False)

plt.figure(figsize=(8, 4))
plot_decision_boundaries(kmeans, X)
plt.show()

print()
print("{:.2f}".format(kmeans.score(X)))
As shown below, the points are clustered well.

The score (-211.60) is printed below the chart. This score is the inertia--the negated sum of the squared distance from the centroids to the data. The model's goal is to maximize this number (making it closer to zero).

The k-Means Algorithm

Execute these commands show the first three iterations of a k-Means model:: 
random_seed = 5

kmeans_iter1 = KMeans(n_clusters=5, init="random", n_init=1, max_iter=1,
                      random_state=random_seed)
kmeans_iter2 = KMeans(n_clusters=5, init="random", n_init=1, max_iter=2,
                      random_state=random_seed)
kmeans_iter3 = KMeans(n_clusters=5, init="random", n_init=1, max_iter=3,
                      random_state=random_seed)
kmeans_iter1.fit(X)
kmeans_iter2.fit(X)
kmeans_iter3.fit(X)

plt.figure(figsize=(10, 8))

plt.subplot(321)
plot_data(X)
plot_centroids(kmeans_iter1.cluster_centers_, circle_color='r', cross_color='w')
plt.ylabel("$x_2$", rotation=0)
plt.tick_params(labelbottom=False)
plt.title("Update the centroids (initially randomly)")

plt.subplot(322)
plot_decision_boundaries(kmeans_iter1, X, show_xlabels=False,
                         show_ylabels=False)
plt.title("Label the instances")

plt.subplot(323)
plot_decision_boundaries(kmeans_iter1, X, show_centroids=False,
                         show_xlabels=False)
plot_centroids(kmeans_iter2.cluster_centers_)

plt.subplot(324)
plot_decision_boundaries(kmeans_iter2, X, show_xlabels=False,
                         show_ylabels=False)

plt.subplot(325)
plot_decision_boundaries(kmeans_iter2, X, show_centroids=False)
plot_centroids(kmeans_iter3.cluster_centers_)

plt.subplot(326)
plot_decision_boundaries(kmeans_iter3, X, show_ylabels=False)

plt.show()

print()
print("{:.2f}".format(kmeans_iter1.score(X)))
print("{:.2f}".format(kmeans_iter2.score(X)))
print("{:.2f}".format(kmeans_iter3.score(X)))
Here's how the k-Means algorithm works:
  1. It starts by randomly placing the centroids
  2. It labels the points by finding the nearest centroid
  3. It updates the centroids to the center of the points in their class
  4. Loop back to step 2 for the next iteration
In just three iterations, it fit the data well, as shown below.

Notice the scores at the bottom: it gets up to -212.9, almost as good as the -211.6 from the ten-iteration model we calculated previously.

Bad Starting Values

Change random_seed from 5 to 2 and run the code above again.

As shown below, the model converges to a bad fit, grouping two clusters together and splitting the rightmost cluster in two.

The score is -220, worse than the previous models.

This is why the first model we made used n_init=10, so it would try ten different random starting centroid sets.

Expanding the Vertical Scale

Execute these commands make a dataset with points in five clusters: 
X_exp = X.copy()
for i in range( len(y) ):
  X_exp[i, 1] = 10.0 * X[i, 1]

def plot_clusters(X, y=None):
    plt.scatter(X[:, 0], X[:, 1], c=y, s=1)
    plt.xlabel("$x_1$")
    plt.ylabel("$x_2$", rotation=0)

plt.figure(figsize=(8, 4))
plot_clusters(X_exp)
plt.gca().set_axisbelow(True)
plt.grid()
plt.show()
As shown below, the chart looks the same but the vertical axis labels are larger.

Fitting a k-Means Model

Execute these commands make a dataset with points in five clusters: 
from sklearn.cluster import KMeans

k = 5
kmeans = KMeans(n_clusters=k, random_state=42, n_init=10)
y_pred = kmeans.fit_predict(X_exp)

def plot_data(X):
    plt.plot(X[:, 0], X[:, 1], 'k.', markersize=2)

def plot_centroids(centroids, weights=None, circle_color='w', cross_color='k'):
    if weights is not None:
        centroids = centroids[weights > weights.max() / 10]
    plt.scatter(centroids[:, 0], centroids[:, 1],
                marker='o', s=35, linewidths=8,
                color=circle_color, zorder=10, alpha=0.9)
    plt.scatter(centroids[:, 0], centroids[:, 1],
                marker='x', s=2, linewidths=12,
                color=cross_color, zorder=11, alpha=1)

def plot_decision_boundaries(clusterer, X, resolution=1000, show_centroids=True,
                             show_xlabels=True, show_ylabels=True):
    mins = X.min(axis=0) - 0.1
    maxs = X.max(axis=0) + 0.1
    xx, yy = np.meshgrid(np.linspace(mins[0], maxs[0], resolution),
                         np.linspace(mins[1], maxs[1], resolution))
    Z = clusterer.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    plt.contourf(Z, extent=(mins[0], maxs[0], mins[1], maxs[1]),
                cmap="Pastel2")
    plt.contour(Z, extent=(mins[0], maxs[0], mins[1], maxs[1]),
                linewidths=1, colors='k')
    plot_data(X)
    if show_centroids:
        plot_centroids(clusterer.cluster_centers_)

    if show_xlabels:
        plt.xlabel("$x_1$")
    else:
        plt.tick_params(labelbottom=False)
    if show_ylabels:
        plt.ylabel("$x_2$", rotation=0)
    else:
        plt.tick_params(labelleft=False)

plt.figure(figsize=(8, 4))
plot_decision_boundaries(kmeans, X_exp)
plt.show()

print()
print("{:.2f}".format(kmeans.score(X)))
As shown below, the model fails. It's counting vertical distance much more than horizontal distance, ruining its ability to fit the data. The score is outrageous.

Preparing a Moon-Shaped Dataset

Execute these commands to create a moon-shaped dataset: 
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split

X, y = make_moons(n_samples=500, noise=0.15, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

def plot_dataset(X, y, axes):
    plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
    plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
    plt.axis(axes)
    plt.grid(True, which='both')
    plt.xlabel(r"$x_1$", fontsize=20)
    plt.ylabel(r"$x_2$", fontsize=20, rotation=0)

plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show()
As shown below, the data consists of two classes which cannot be separated by a simple line.

Flag ML 116.1: Fitting the Moons (15 pts)

Use the moon-shaped dataset you just created.

Start with the second block of code near the top of this project, titled "Fitting a k-Means Model".

Fit a k-Means model to the data with these parameters:

  • k = 8
  • random_state=1
  • n_init=5
  • max_iter=4 (add this parameter inside the KMeans() call)
Make sure you are using the original data (X), not the data with the expanded vertical scale (X_exp). You need to change that in two places.

The flag is covered by a green rectangle in the image below.

Using Clustering for Semi-Supervised Learning

We're going to use a dataset with 1,797 images, but only use 50 labels.

Preparing the Digits Dataset

Execute these commands prepare a dataset with 1,797 grayscale 8x8 imeges of handwritten digits: 
from sklearn.datasets import load_digits
import matplotlib.pyplot as plt

X_digits, y_digits = load_digits(return_X_y=True)
X_train, y_train = X_digits[:1400], y_digits[:1400]
X_test, y_test = X_digits[1400:], y_digits[1400:]

plt.figure(figsize=(8, 2))
for row in range(5):
  line = ""
  for column in range(10):
    plt.subplot(5, 10, 10*row + column + 1)
    plt.imshow(X_train[10*row + column].reshape(8, 8), cmap="binary",
               interpolation="bilinear")
    plt.axis('off')
plt.show()
print()
for row in range(5):
  line = ""
  for column in range(10):
    line += str(y_train[10*row + column]) + " "
  print(line)
The first 50 images are displayed, as shown below, followed by the labels.

Fitting a Model to the Training Set

Execute these commands fit a Logistic Regression model to the entire training set of 1400 images with labels. 
from sklearn.linear_model import LogisticRegression

n_labeled = 1400
log_reg = LogisticRegression(max_iter=10_000)
log_reg.fit(X_train[:n_labeled], y_train[:n_labeled])

print("{:.4f}".format(log_reg.score(X_test, y_test)))
As shown below, the model is 90.68% accurate.

Fitting a Model to 50 Instances

Suppose we don't have labeled data, and it's expensive to apply labels. How well can we model this with only 50 labeled images?

Execute these commands fit a Logistic Regression model to just the first 50 images, with labels. 

from sklearn.linear_model import LogisticRegression

n_labeled = 50
log_reg = LogisticRegression(max_iter=10_000)
log_reg.fit(X_train[:n_labeled], y_train[:n_labeled])

print("{:.4f}".format(log_reg.score(X_test, y_test)))
As shown below, the model is 74.81% accurate--much inferior to the model using 1400 labels.

Using a k-Means Model to form 50 Clusters

Let's group similar images together. We don't need labels to do that.

Execute these commands to group the images into 50 clusters using a k-Means model.

We find the "representative" images closest to the centroids and display them. 

from sklearn.cluster import KMeans

k = 50
kmeans = KMeans(n_clusters=k, random_state=42, n_init=10)
X_digits_dist = kmeans.fit_transform(X_train)
representative_digit_idx = X_digits_dist.argmin(axis=0)
X_representative_digits = X_train[representative_digit_idx]

plt.figure(figsize=(8, 2))
for index, X_representative_digit in enumerate(X_representative_digits):
    plt.subplot(k // 10, 10, index + 1)
    plt.imshow(X_representative_digit.reshape(8, 8), cmap="binary",
               interpolation="bilinear")
    plt.axis('off')

plt.show()
The representative images appear, as shown below.

Labelling the 50 Representative Images and Training From Them

We can manually label these images.

Execute the code below to insert the manually determined labels and train a Logistic Regression model on just them. 

import numpy as np

y_representative_digits = np.array([
    1, 3, 6, 0, 7, 9, 2, 4, 8, 9,
    5, 4, 7, 1, 2, 6, 1, 2, 5, 1,
    4, 1, 3, 3, 8, 8, 2, 5, 6, 9,
    1, 4, 0, 6, 8, 3, 4, 6, 7, 2,
    4, 1, 0, 7, 5, 1, 9, 9, 3, 7
])

log_reg = LogisticRegression(max_iter=10_000)
log_reg.fit(X_representative_digits, y_representative_digits)
print("{:.4f}".format(log_reg.score(X_test, y_test)))
The model's accuracy is now increased to 84.89% as shown below.

It's far better to learn from 50 selected representative images than from simply the first 50 images.

Propagating Labels to All Instances

Since we've already grouped the images into 50 clusters, and labeled those 50 clusters, we can label all the images.

Execute the code below to propagate the labels and train the model on the newly labelled 1400 images: 

y_train_propagated = np.empty(len(X_train), dtype=np.int64)
for i in range(k):
    y_train_propagated[kmeans.labels_ == i] = y_representative_digits[i]

log_reg = LogisticRegression(max_iter=10_000)
log_reg.fit(X_train, y_train_propagated)

print("{:.4f}".format(log_reg.score(X_test, y_test)))
The model's accuracy is now increased to over 89% as shown below.

Removing Outliers

We can improve the model even more by excluding outliers--the 1% of the instances that are furthest from their centroids.

Execute this code: 

percentile_closest = 99

X_cluster_dist = X_digits_dist[np.arange(len(X_train)), kmeans.labels_]
for i in range(k):
    in_cluster = (kmeans.labels_ == i)
    cluster_dist = X_cluster_dist[in_cluster]
    cutoff_distance = np.percentile(cluster_dist, percentile_closest)
    above_cutoff = (X_cluster_dist > cutoff_distance)
    X_cluster_dist[in_cluster & above_cutoff] = -1

partially_propagated = (X_cluster_dist != -1)
X_train_partially_propagated = X_train[partially_propagated]
y_train_partially_propagated = y_train_propagated[partially_propagated]


log_reg = LogisticRegression(max_iter=10_000)
log_reg.fit(X_train_partially_propagated, y_train_partially_propagated)

print("{:.4f}".format(log_reg.score(X_test, y_test)))
The model's accuracy is now increased to 90.93%% as shown below. It's as good as using the original labeled training set.

Flag ML 116.2: 20 Clusters (15 pts)

Repeat the whole thing with only 20 clusters, as summarized below:
  1. Preparing the Digits Dataset: exactly as above
  2. Fitting a Model to the Training Set: exactly as above
  3. Fitting a Model to 50 Instances: change n_labeled to 20
  4. Using a k-Means Model to form 50 Clusters: change to 20 clusters
  5. Labelling the 50 Representative Images and Training From Them: add 20 labels you determine manually. DO NOT USE THE LABELS SHOWN ABOVE! The accuracy is 80.86%
  6. Propagating Labels to All Instances: exactly as above. The accuracy increases.
  7. Removing Outliers: exactly as above.

The flag is covered by a green rectangle in the image below.

References

Chapter 9 - Unsupervised Learning

Posted 10-6-23
Image fixed 10-15-23
Flag 1 instructions augmented, video added 10-21-23
Hint added to flag 1 and minor text changes 12-12-23
Flag 2, step 3, changed in a minor way 7-24-24
Scikit-learn version installation added 8-12-24