ML 112: Support Vector Machines (40 pts extra)

What You Need

Purpose

To observe the effect of feature scaling on linear Support Vector Machines.

Using Google Colab

In a browser, go to
https://colab.research.google.com/
If you see a blue "Sign In" button at the top right, click it and log into a Google account.

From the menu, click File, "New notebook".

Preparing a Dataset

Execute these commands to create a simple, artificial dataset consisting of two groups of points in a plane. 
!pip install secml
import secml
random_state = 999

n_features = 2  # Number of features
n_samples = 125  # Number of samples
centers = [[-1.1, -2], [1.5, 1.6]]  # Centers of the clusters
cluster_std = 0.7  # Standard deviation of the clusters

from secml.data.loader import CDLRandomBlobs
dataset = CDLRandomBlobs(n_features=n_features, 
                         centers=centers, 
                         cluster_std=cluster_std,
                         n_samples=n_samples,
                         random_state=random_state).load()

n_tr = 100  # Number of training set samples
n_ts = 25  # Number of test set samples

# Split in training and test
from secml.data.splitter import CTrainTestSplit
splitter = CTrainTestSplit(
    train_size=n_tr, test_size=n_ts, random_state=random_state)
tr, ts = splitter.split(dataset)
print()

from secml.figure import CFigure
# Only required for visualization in notebooks
%matplotlib inline

fig = CFigure(width=5, height=5)

# Convenience function for plotting a dataset
fig.sp.plot_ds(tr)

fig.show()
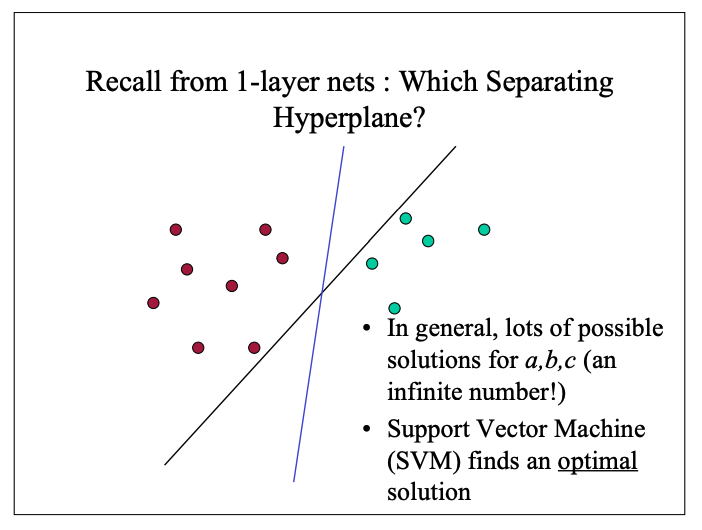
As shown below, you see two categories of dots, shown in different colors.

The task of this model is to sort the dots into their categories.

Creating and Training the Model

Execute these commands to create and train the linear SVM model: 
from secml.ml.classifiers import CClassifierSVM
svm = CClassifierSVM()

svm.fit(tr.X, tr.Y)

# Compute predictions on a test set
y_pred = svm.predict(ts.X)

# Metric to use for training and performance evaluation
from secml.ml.peval.metrics import CMetricAccuracy
metric = CMetricAccuracy()

# Evaluate the accuracy of the classifier
acc = metric.performance_score(y_true=ts.Y, y_pred=y_pred)

print("Accuracy on test set: {:.2%}".format(acc))
print("Weights: ", svm.w)
print()

fig = CFigure(width=5, height=5)

# Convenience function for plotting the decision function of a classifier
fig.sp.plot_decision_regions(svm, n_grid_points=200, grid_limits=[(-3,3),(-4,4)])

fig.sp.plot_ds(tr)
fig.sp.grid(grid_on=True)

fig.sp.title("Scale of X and Y Similar")
fig.show()
As shown below, the model has 100% accuracy, and it fits a diagonal line that correctly divides the centers of the classes.

Also, the weights of the X and Y features are similar, since they are both equally useful at distinguishing the classes.

Expanding the Y Scale

Execute these commands to multiply the Y axis by 100. 
tr_exp = tr.deepcopy()
for i in range(n_tr):
  tr_exp.X[i,1] = 100.0 * tr.X[i,1]
ts_exp = ts.deepcopy()
for i in range(n_ts):
  ts_exp.X[i,1] = 100.0 * ts.X[i,1]

from secml.figure import CFigure
# Only required for visualization in notebooks
%matplotlib inline

fig = CFigure(width=5, height=5)

# Convenience function for plotting a dataset
fig.sp.plot_ds(tr_exp)

fig.show()
As shown below, the data is the same, but the Y-axis is magnified.

Creating and Training the Model

Execute these commands to create and train the linear SVM model: 
from secml.ml.classifiers import CClassifierSVM
svm = CClassifierSVM()

svm.fit(tr_exp.X, tr_exp.Y)

# Compute predictions on a test set
y_pred = svm.predict(ts_exp.X)

# Metric to use for training and performance evaluation
from secml.ml.peval.metrics import CMetricAccuracy
metric = CMetricAccuracy()

# Evaluate the accuracy of the classifier
acc = metric.performance_score(y_true=ts_exp.Y, y_pred=y_pred)

print("Accuracy on test set: {:.2%}".format(acc))
print("Weights: ", svm.w)
print()

fig = CFigure(width=5, height=5)

# Convenience function for plotting the decision function of a classifier
fig.sp.plot_decision_regions(svm, n_grid_points=200, grid_limits=[(-3.5,3.5),(-500,500)])

fig.sp.plot_ds(tr_exp)
fig.sp.grid(grid_on=False)

fig.sp.title("Scale of X and Y Different")
fig.show()
As shown below, the model has 100% accuracy, but it fits a more horizontal decision line, because vertical gaps between the support vectors and the decision line are considered more important than horizontal gaps.

Also, the weights of the X and Y features are very different.

Flag ML 112.1: Different Y Scale (10 pts)

Repeat the process above, but change the Y magnification in the third block of code from 100 to 10.

The flag is the weight for the Y feature, covered by a green rectangle in the image below.

A Dataset that Overlaps

Execute these commands to create a dataset with classes that overlap, so they must be fit with soft margin classification. 
!pip install secml
import secml
random_state = 999

n_samples = 100  # Number of samples

n_features = 2  # Number of features

centers = [[-1.1, -2], [1.5, 1.6]]  # Centers of the clusters
cluster_std = 1.2  # Standard deviation of the clusters

from secml.data.loader import CDLRandomBlobs
dataset = CDLRandomBlobs(n_features=n_features, 
                         centers=centers, 
                         cluster_std=cluster_std,
                         n_samples=n_samples,
                         random_state=random_state).load()

n_tr = 80  # Number of training set samples
n_ts = 20  # Number of test set samples

# Split in training and test
from secml.data.splitter import CTrainTestSplit
splitter = CTrainTestSplit(
    train_size=n_tr, test_size=n_ts, random_state=random_state)
tr, ts = splitter.split(dataset)
print()

from secml.figure import CFigure
# Only required for visualization in notebooks
%matplotlib inline

fig = CFigure(width=5, height=5)

# Convenience function for plotting a dataset
fig.sp.plot_ds(tr)

fig.show()
As shown below, the categories of dots overlap. This data cannot be perfectly sorted with any line. We'll use soft margin classification to find the best linear SVM model.

Creating and Training the Model

Execute these commands to create and train the linear SVM model, with various values of C. 
from secml.ml.classifiers import CClassifierSVM
from secml.ml.peval.metrics import CMetricAccuracy
metric = CMetricAccuracy()

for cc in [0.0001, 0.001, 0.01, 0.1, 1]:
  svm = CClassifierSVM(C=cc)
  svm.fit(tr.X, tr.Y)
  y_pred = svm.predict(ts.X)
  acc = metric.performance_score(y_true=ts.Y, y_pred=y_pred)
  print()
  print("C:", cc, "Accuracy on test set: {:.2%}".format(acc))
  print("Weights: ", svm.w)
  print()

  fig = CFigure(width=5, height=5)
  fig.sp.plot_decision_regions(svm, n_grid_points=200, grid_limits=[(-4,4),(-6,7)])
  fig.sp.plot_ds(tr)
  fig.sp.grid(grid_on=True)
  fig.sp.title("C: " + str(cc))
  fig.show()
Scroll through the output to see the various solutions. As shown below, the lowest value of C simply sorts every instance into the "Blue" category, but the larger C values find goof solutions.

Flag ML 112.2: Larger Standard Deviation (10 pts)

Repeat the process above, but change the standard deviation "cluster_std" from 1.2 to 2.0.

The flag is the weight for the Y feature, covered by a green rectangle in the image below.

A Dataset that Curves

Execute these commands to create a dataset with a curved boundary between them, so a nonlinear model will be required. 
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.15, random_state=42)

def plot_dataset(X, y, axes):
    plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
    plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
    plt.axis(axes)
    plt.grid(True, which='both')
    plt.xlabel(r"$x_1$", fontsize=20)
    plt.ylabel(r"$x_2$", fontsize=20, rotation=0)

plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show()
As shown below, the dots form two interlocking curves.

Creating and Training the Model

Execute these commands to create and train the linear SVM model, with polynomial features added. 
import numpy as np

from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.svm import LinearSVC
polynomial_svm_clf = Pipeline([
        ("poly_features", PolynomialFeatures(degree=3)),
        ("scaler", StandardScaler()),
        ("svm_clf", LinearSVC(C=10, loss="hinge", random_state=42, max_iter=10000))
    ])

polynomial_svm_clf.fit(X, y)
A diagrem of the pipeline appears, as shown below.

Showing the Decision Boundary

Execute these commands to show the decision boundary. 
def plot_predictions(clf, axes):
    x0s = np.linspace(axes[0], axes[1], 100)
    x1s = np.linspace(axes[2], axes[3], 100)
    x0, x1 = np.meshgrid(x0s, x1s)
    X = np.c_[x0.ravel(), x1.ravel()]
    y_pred = clf.predict(X).reshape(x0.shape)
    y_decision = clf.decision_function(X).reshape(x0.shape)
    plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2)
    plt.contourf(x0, x1, y_decision, cmap=plt.cm.brg, alpha=0.1)

print()
print(polynomial_svm_clf.decision_function([(0,0)]))
print()

plot_predictions(polynomial_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])

plt.show()
As shown below, the model fits the data well. The number above the chart is the decision function at the origin, printed just to act as a flag later.

Flag ML 112.3: Second Degree (10 pts)

Repeat the process above, but change the degree of the polynomial from 3 to 2.

This makes the model much worse.

The flag is the decision function at the origin, covered by a green rectangle in the image below.

Polynomial Kernels

Use the same data generated above, in the "A Dataset that Curves" section.

Execute these commands to use the "Kernel Trick" to fit a model which is as good as one with polynomial features added, but much faster to compute. 

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC

poly_kernel_svm_clf = Pipeline([
        ("scaler", StandardScaler()),
        ("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
    ])
poly_kernel_svm_clf.fit(X, y)
A diagram of the pipeline appears, as shown below.

Showing the Decision Boundary

Execute these commands to show the decision boundary. 
import numpy as np

def plot_predictions(clf, axes):
    x0s = np.linspace(axes[0], axes[1], 100)
    x1s = np.linspace(axes[2], axes[3], 100)
    x0, x1 = np.meshgrid(x0s, x1s)
    X = np.c_[x0.ravel(), x1.ravel()]
    y_pred = clf.predict(X).reshape(x0.shape)
    y_decision = clf.decision_function(X).reshape(x0.shape)
    plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2)
    plt.contourf(x0, x1, y_decision, cmap=plt.cm.brg, alpha=0.1)

print()
print(poly_kernel_svm_clf.decision_function([(0,0)]))
print()

plot_predictions(poly_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])

plt.show()
As shown below, the model fits the data well, just like the 3rd degree polynomial you calculated previously.

Flag ML 112.4: Tenth Degree (10 pts)

Repeat the process above, but change the degree of the polynomial from 3 to 10. Also change "coef0" from 1 to 100.

The flag is the decision function at the origin, covered by a green rectangle in the image below.

References

Chapter 5 -- Support Vector Machines

Posted 9-17-23
Video added 10-21-23