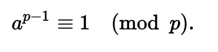
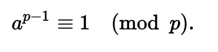
So testing that condition for several random values of a can be used as evidence that p is probably prime.
This site explains the Fermat primality test and its flaws in more detail:
https://en.wikipedia.org/wiki/Fermat_primality_test
from random import randint
p = int(raw_input("Input potential prime: "))
for i in range(5):
a = randint(2,p-2)
if pow(a, p-1, p) == 1:
print "Test passed for ", a
else:
print "Test failed for ", a
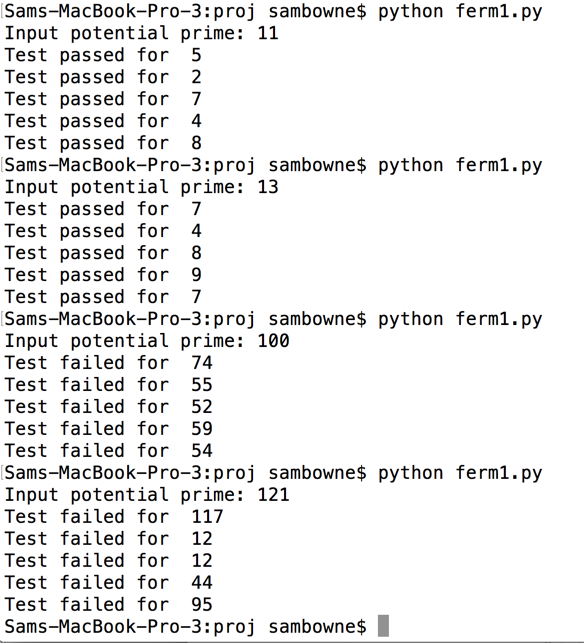
As shown below, 11 and 13 pass all the tests because they are prime, but 100 and 121 fail because they aren't.
149893897637335061961928327350470188799927663887947357440069371232471599832948115772987524239902313942376737764843434513577954709550540438646101225413150283056505892203493267823497754444007029293809481459043218629633809451460944629963616409822735245271280411960104440928839926847578561621781631648006307217641
It works, because Python really can handle any size of integer, as shown below.

10**300
Find the first number above it which is prime.
Use the form below to put your name on the WINNERS PAGE.
Find the first set of companion primes above
10**100
Use the form below to put your name on the WINNERS PAGE.