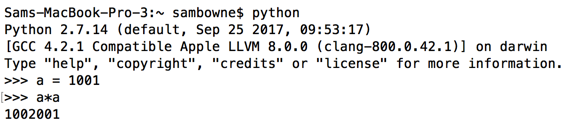
python
a = 1001
a*a

a = 10**100 + 1
a*a

a = 10**100 + 1
b = a * a
import math
math.sqrt(b)

To see that, execute these commands at the Python prompt:
a = 10**100 + 1
b = a * a
from decimal import *
getcontext().prec = 200
Decimal(b).sqrt()

10000000000000000016800000000000000005031
To find the square root, execute these commands at the Python prompt:
n = 10000000000000000016800000000000000005031
from decimal import *
getcontext().prec = 50
Decimal(n).sqrt()

So one way to find a factor is to test all odd numbers below the square root.
To do that, execute these commands at the Python prompt. Press Enter twice after the last command.
n = 10000000000000000016800000000000000005031
p0 = 100000000000000000083
for p in range(p0, p0-80, -2):
print p, n%p

n = 10000000000000000016800000000000000005031
p = 100000000000000000039
q = n/p
print q
print p * q
print n - p * q

The factors are:
p = 100000000000000000039
q = 100000000000000000129
As shown above, the square root of n is 100000000000000000083 (plus a fraction).
As expected, one factor is above the square root and the other is below it.
123459259296296790129629703704567911111222220989329646370537655992609296463211544461111289984805767
Use the form below to put your name on the WINNERS PAGE.
2457319490775870034107936327697724401721210936487723795115696610653082228345978452724879092419462602801287921034412592451829320597304383170626854710604026609207557310932504074259543909051122202199219
Use the form below to put your name on the WINNERS PAGE.