At the top is the pure state |0>
and at the bottom is the pure state |1>.
Normal computers use bits with only these two states: 0 and 1.
Quantum computers use the whole range of states, including the
intermediate states that are "superpositions" of |0> and |1>.
In a Web browser, go to
https://quantumexperience.ng.bluemix.net/qx/experience
Click the "Start experimenting with a quantum computer" button, as shown below.
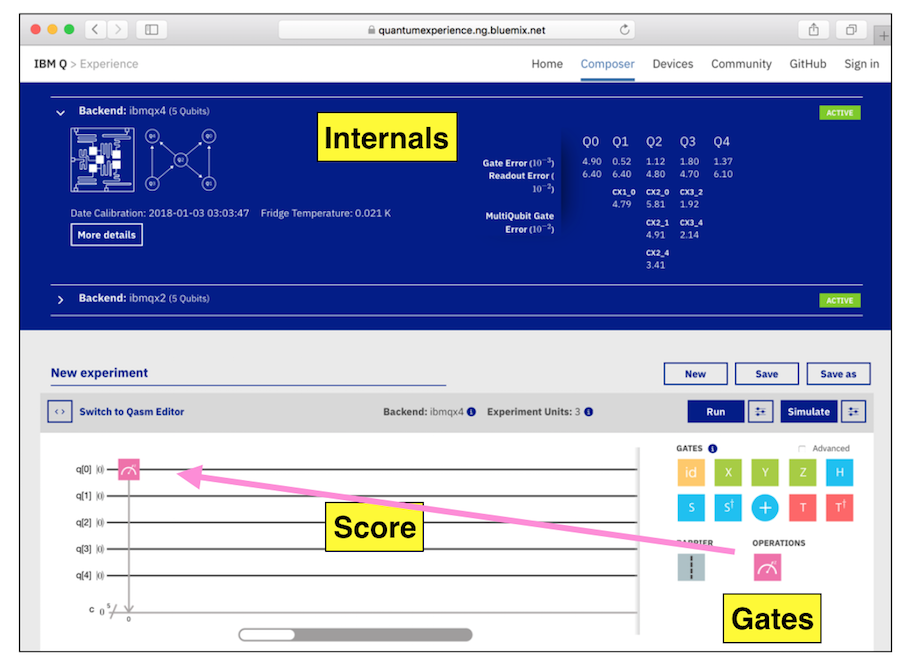
The next page shows the "Composer". Here we'll program a quantum computer, using the chart at the bottom with five lines, like a music composer's score.
At the top is the Internals section, showing the details of IBM's actual quantum computer. Ignore it for this project.
At the lower left is the Score where you will create your programs, by dragging Gates from the right and dropping them.
The pink icon with a white umbrella-looking figure on it is called a "Measurement Gate". Drag a measurement gate onto the score and drop it there, as indicated by the pink arrow in the figure below.
At the center right, click the Simulate button.
A login box pops up, as shown below. Log in with a social network, or create an IBM Q account and log in with that.
It puts you on a forum page. Refresh the page to implement the log in. Then, from the top menu, click Learn, Composer, as shown below.
Drag the pink "Measurement Gate" onto the score and drop it there again.
Click the Simulate button.
A box pops up asking you to "Name your experiment". Click OK.
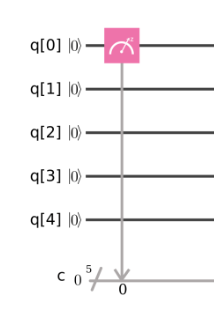
"Your Quantum Results" appear, including the "Quantum State: Computation Basis" chart shown below.
This chart shows the results of running your experiment 100 times. Every time, the result was the same: 00000, as shown at the bottom of the purple bar.

It did not demonstrate any quantum behavior. There are five Qubits, and they all start in the "Zero" state, written as
|0>
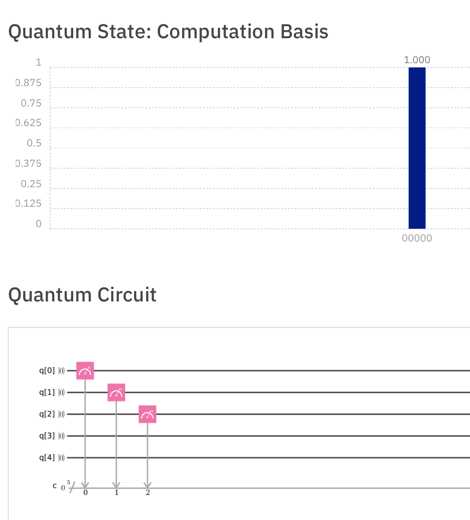
Click the Simulate button. You get the same result: 00000 every time, as shown in the upper part of the image below.
This is how ordinary non-quantum processors work. Measuring a bit has no effect on it--you can measure it anytime you want.
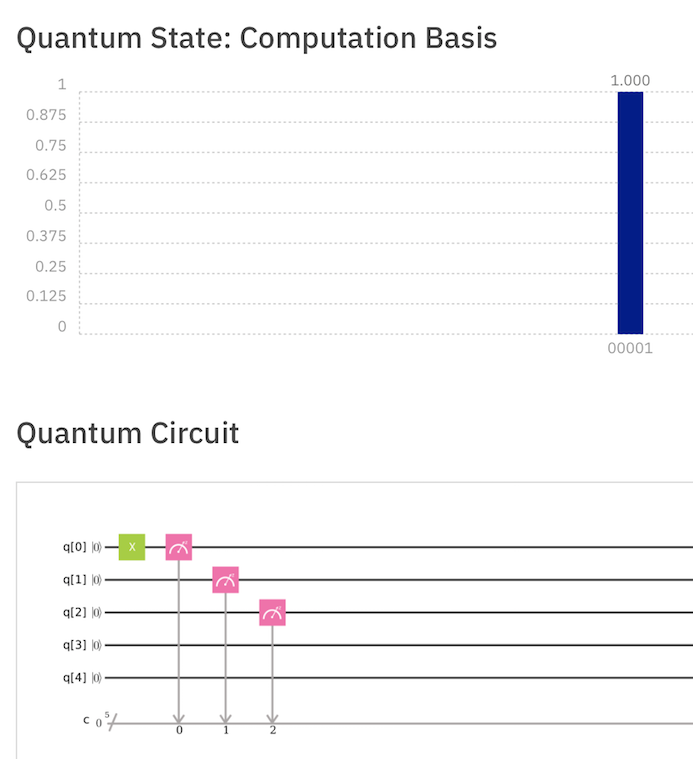
Drag gates as needed to make the quantum score shown below, and Simulate it.
The green X gate flips a Qubit from
|0>
to
|1>
This is still the same as a normal processor: no quantum effects are visible.
Drag gates as needed to make the quantum score shown below, and Simulate it.
The blue H gate
is called a "Hadamard" gate, and it changes
a Qubit from its
|0>
state to a "Superposition" state,
mixing equal portions of the
|0>
state and the
|1>
state.
This is also called "Uncertainty" and it's the bizarre part of quantum mechanics: quantum objects in a "Superposition" state are neither 1 nor 0, but in an uncertain state with a probability of either result.
So the measurement doesn't always give the same result. Half the time the result is 00001 and the other half of the time it's 00000.
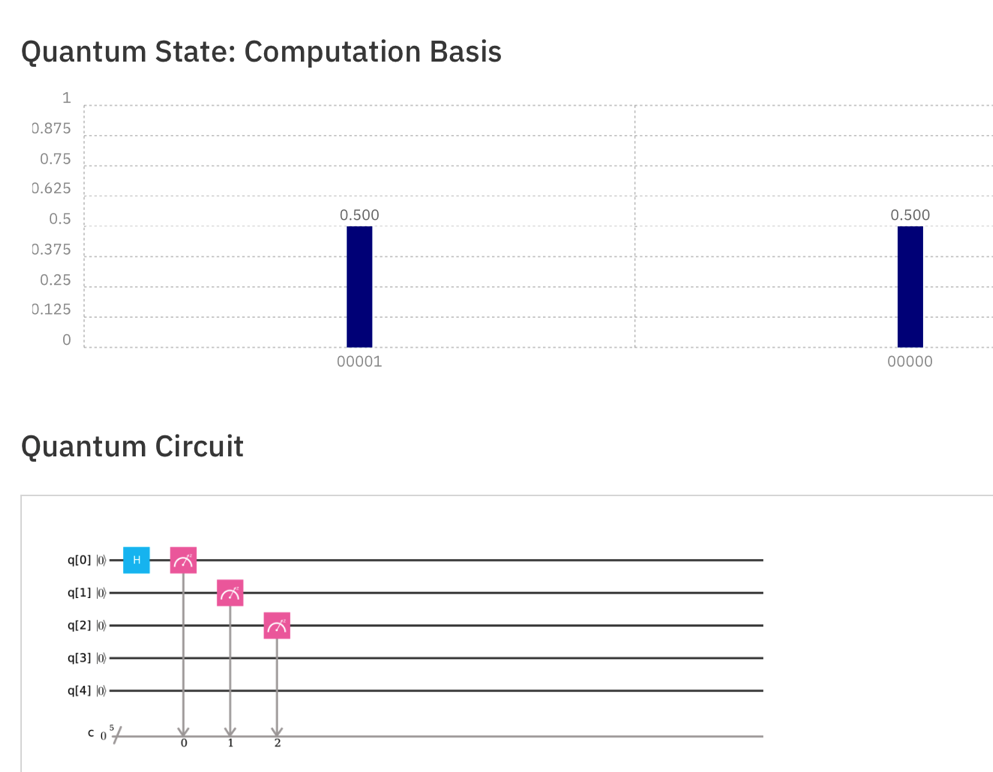
Drag gates as needed to make the quantum score shown below, and Simulate it.
The three Qubits are all in Superposition states, so there are eight possible results with equal probability.
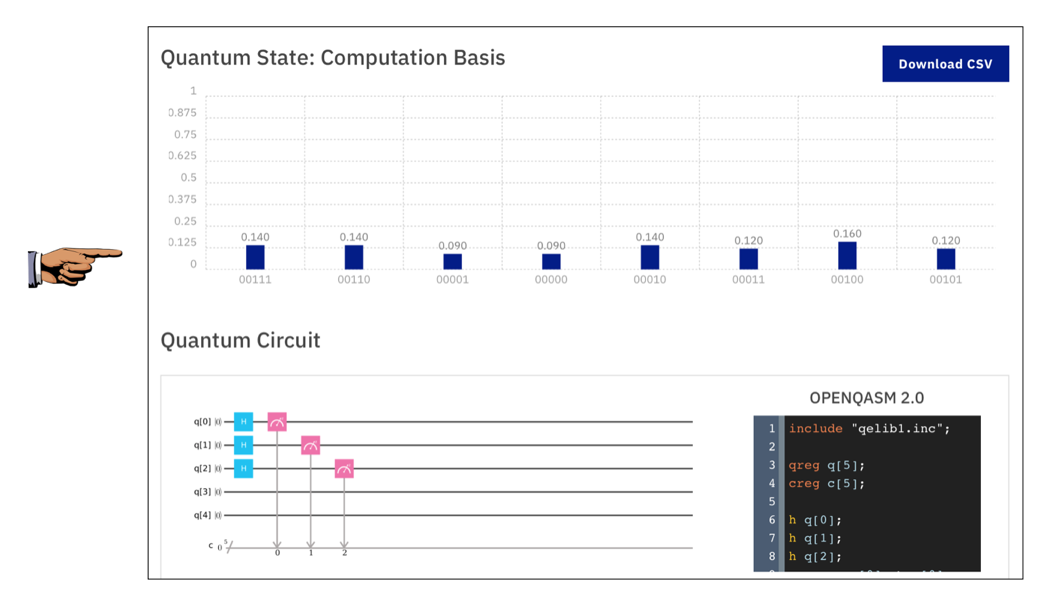
Drag gates as needed to make the quantum score shown below, and Simulate it.
The H gate makes the second Qubit
uncertain, but the other two Qubits are
stable in the
|0>
state,.
The only two possible answers are 00000 and 00010, as shown below.
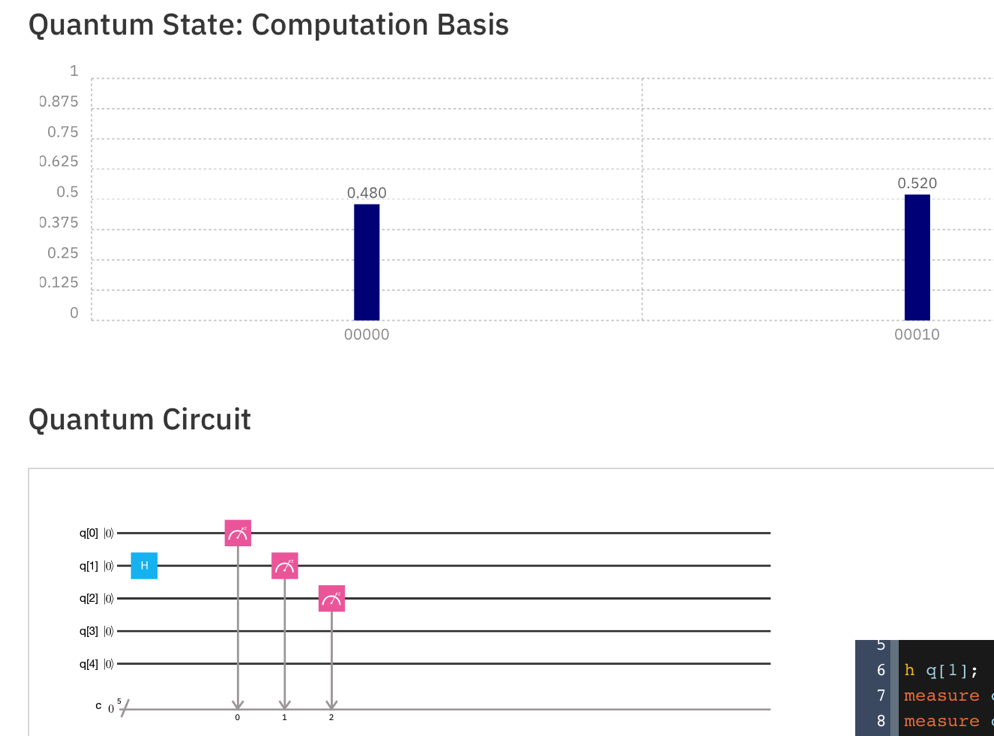
Drag gates as needed to make the quantum score shown below, and Simulate it.
The + gate Entangles two Qubits, so they will always give the same result when measured. So Qubit 0 now follows Qubit 1, and the possible results are now 00000 and 00011, as shown below.
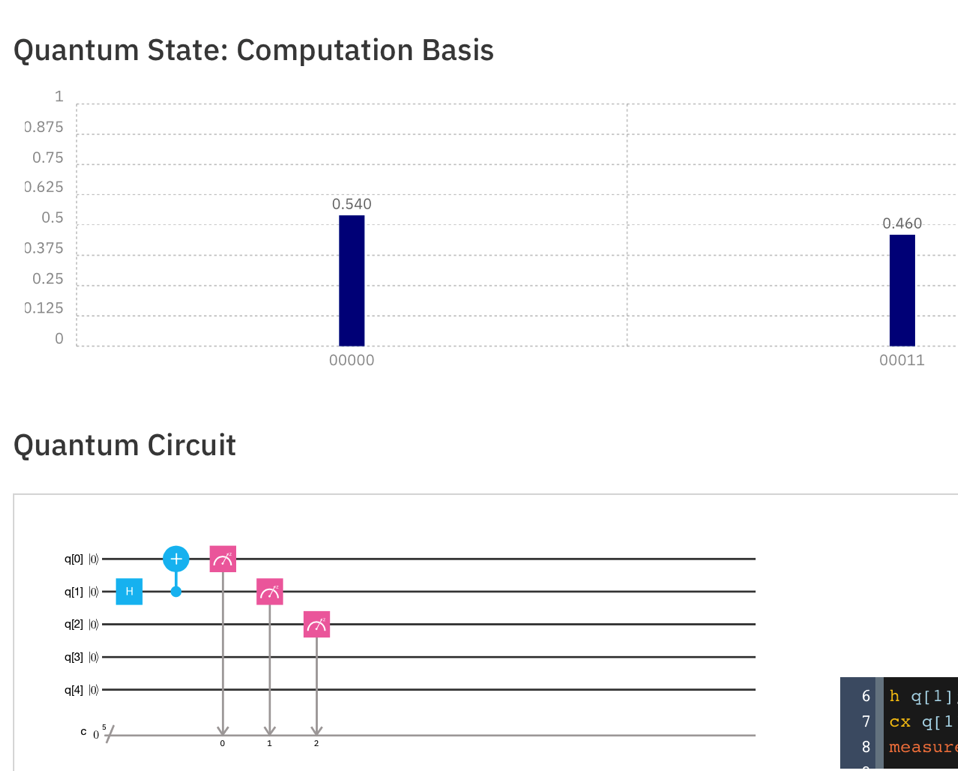
Drag gates as needed to make the quantum score shown below, and Simulate it.
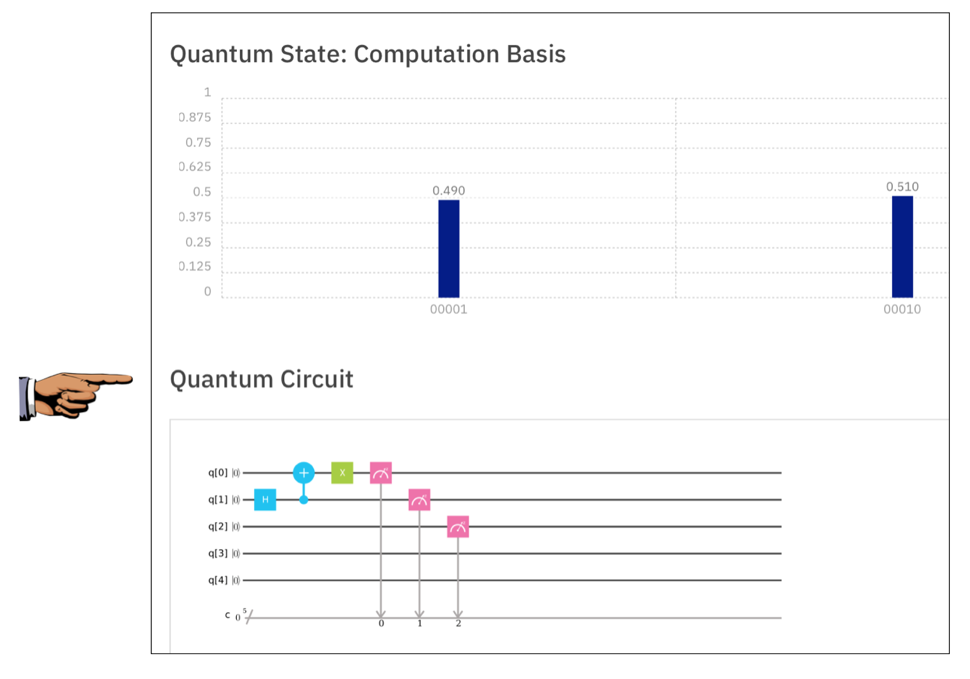
Now Qubits 0 and 1 are entangled, but always opposite, so the possible results are 00001 and 00010, as shown below.
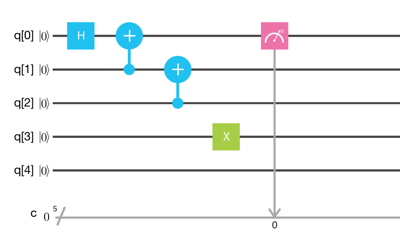
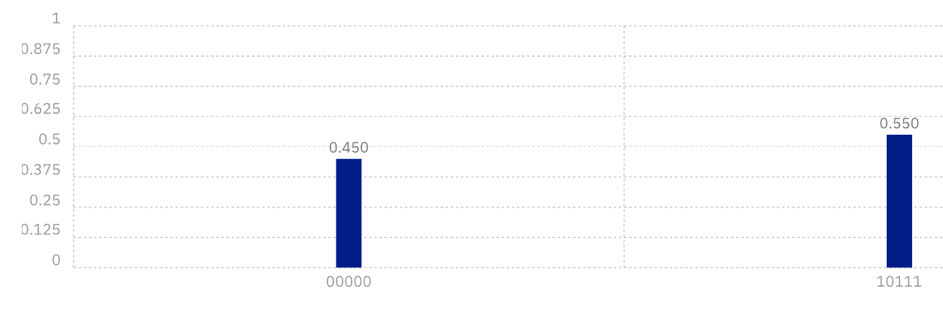
One of my students succeeded in entangling all five Qubits.
This is interesting, but it's not worth any points in Crypto Hero because I couldn't figure out anything to submit to prove you completed it.
Posted 1-3-18 by Sam Bowne
Added to Crypto Hero 4-16-18 8:45 am
Image added to make challenge possible 6-2-18
Background added 8-10-18
Login process updated 3-5-19