Proj 14: Padding Oracle Attack (15 pts. + 20 pts. extra credit)

What You Need

Any machine with Python 2.7. I used a Mac. The easiest machine to set up is probably Kali or Ubuntu Linux.

Purpose

To learn how the Padding Oracle attack works against AES-CBC.

Background

Encrypting 48 Bytes

Cipher Block Chaining is diagrammed below (image based on one from Wikipedia).

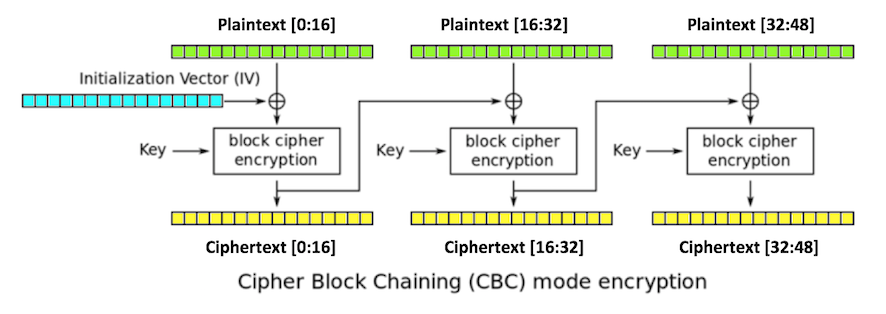
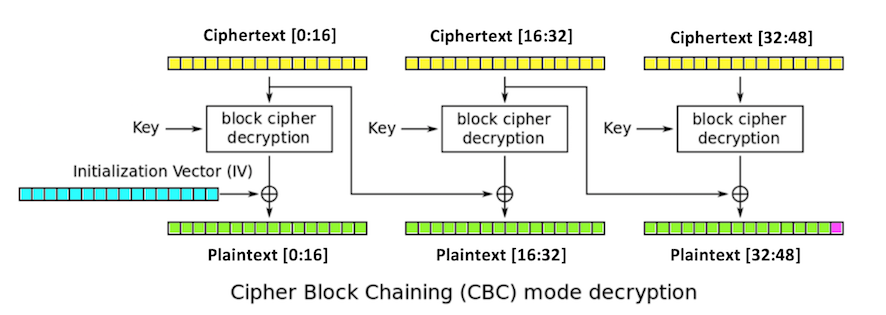
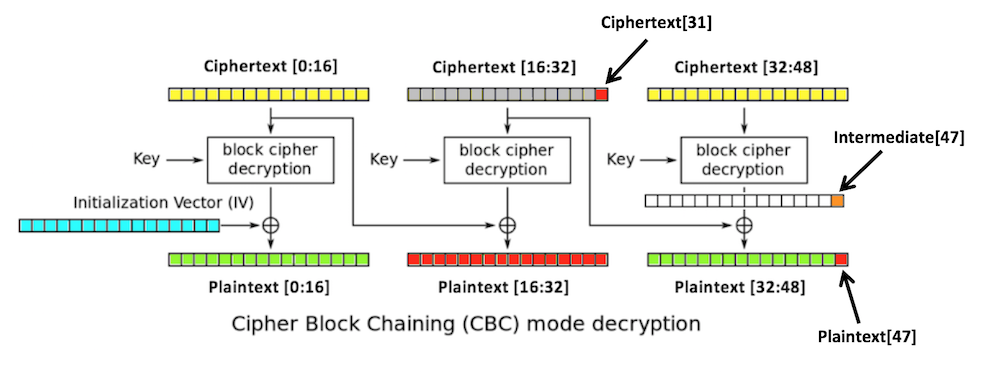
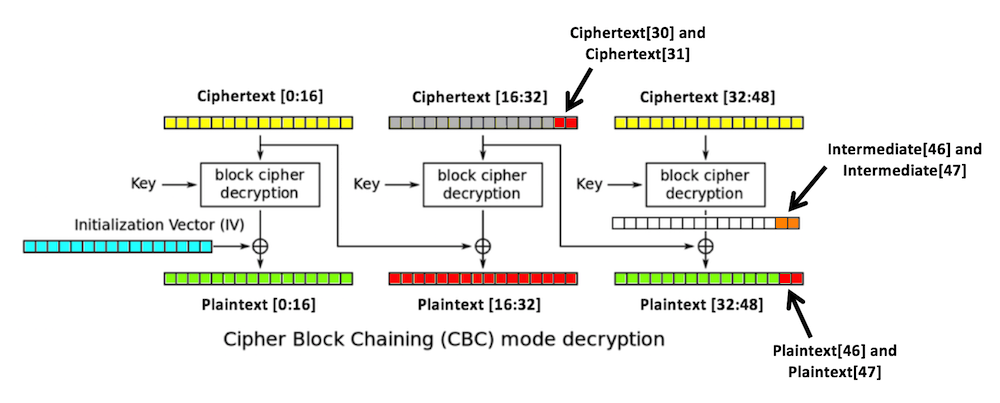
Three blocks of plaintext (green), each 16 bytes long, are encrypted, producing three blocks of ciphertext (yellow).

The first block is XORed with an initialization vector or iv (blue), also 16 bytes long, and then encrypted with the key.

Each subsequent block is XORed with the previous block of ciphertext.

Encrypting 47 Bytes

Suppose the plaintext is only 47 bytes long. In that case, a byte of padding (purple) must be added, as shown below.

Decryption

Using the same key and iv (blue), the ciphertext (yellow) can be decrypted to find the plaintext (green). The last byte is the padding (purple), as shown below.

Padding with PKCS #7

A common system of padding is Public Key Cryptography Standard #7, or PKCS #7. It works like this: So in the diagram above, this Python condition is true:
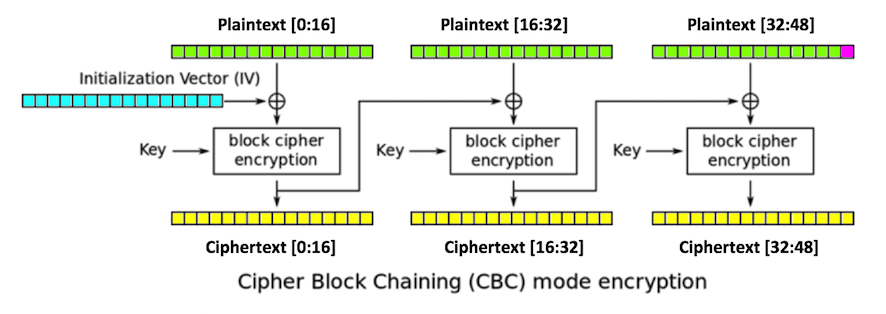
plaintext[47] == chr(1)

Modifying a Byte of Ciphertext

Suppose we modify:
ciphertext[31]
That will garble the whole second block of plaintext:
plaintext[16:32]
But it will only change a single byte of the third block:
plaintext[47]
This is shown below, with red indicating changed bytes.

Demonstration in Python

Starting Python

Open a Terminal or Command Prompt and execute this command to open Python in interactive mode: 
python

Setting Initial Values

Enter these commands to prepare the environment for encryption, as shown below. 
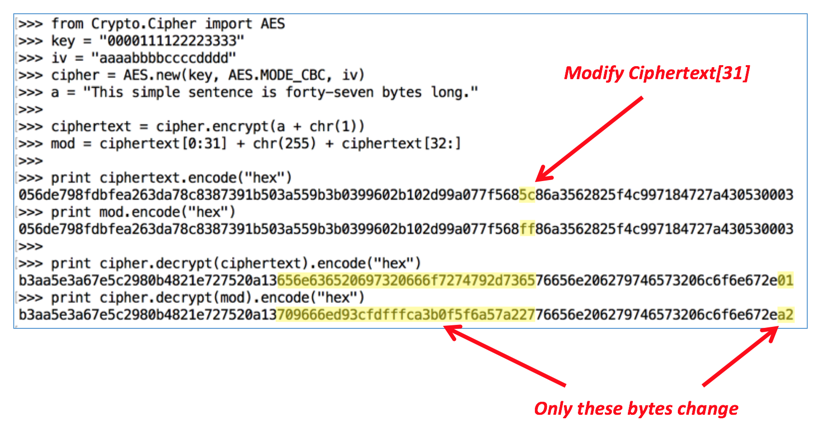
from Crypto.Cipher import AES
key = "0000111122223333"
iv = "aaaabbbbccccdddd"
cipher = AES.new(key, AES.MODE_CBC, iv)
a = "This simple sentence is forty-seven bytes long."

Padding and Encrypting

Enter these commands to pad the sentence and encrypt it, placing the result in "ciphertext", and make a modified ciphertext string named "mod" with ciphertext[31] changed to chr(255), as shown below. 
ciphertext = cipher.encrypt(a + chr(1))
mod = ciphertext[0:31] + chr(255) + ciphertext[32:]

Viewing the Modified Ciphertext

Enter these commands to print the original and modified ciphertext in hexadecimal encoding, so it is eash to see the single byte that is changed, as highlighted in the image below. 
print ciphertext.encode("hex")
print mod.encode("hex")

Viewing the Decrypted Text

Enter these commands to decrypt the original and modified ciphertext, printing the results in hexadecimal encoding. As highlighted below, the second block and the padding byte change, but nothing else. 
print cipher.decrypt(ciphertext).encode("hex")
print cipher.decrypt(mod).encode("hex")

Making a Vulnerable System

Making the Pador Functions

This is a simple AES-CBC implementation that encrypts and decrypts. If the decrypted text is not properly padded, it returns an error message. This is the way many encryption implementations have been written.

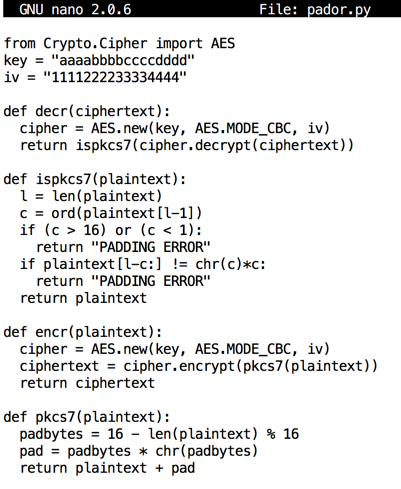
Use a text editor, such as nano or Notepad, to make this file. Save it as pador.py in your home directory. 

from Crypto.Cipher import AES
key = "aaaabbbbccccdddd"
iv = "1111222233334444"

def decr(ciphertext):
  cipher = AES.new(key, AES.MODE_CBC, iv)
  return ispkcs7(cipher.decrypt(ciphertext))

def ispkcs7(plaintext):
  l = len(plaintext)
  c = ord(plaintext[l-1])                       
  if (c > 16) or (c < 1):
    return "PADDING ERROR"
  if plaintext[l-c:] != chr(c)*c:
    return "PADDING ERROR"
  return plaintext

def encr(plaintext):
  cipher = AES.new(key, AES.MODE_CBC, iv)
  ciphertext = cipher.encrypt(pkcs7(plaintext))
  return ciphertext

def pkcs7(plaintext):
  padbytes = 16 - len(plaintext) % 16
  pad = padbytes * chr(padbytes)
  return plaintext + pad

Starting Python

Open a Terminal or Command Prompt and execute this command to open Python in interactive mode: 
python

Encrypting a 47-Byte Plaintext

Enter these commands to encrypt a sentence, and show the encrypted string in hexadecimal encoding, as shown below. 
from pador import encr, decr
a = "This simple sentence is forty-seven bytes long."
c = encr(a)
print c.encode("hex")
As shown below, the encrypted string is a long random series of hexadecimal values.

Decrypting the Ciphertext

Enter these commands to decrypt the ciphertext, and show the result in ASCII and in hexadecimal encoding, as shown below. 
d = decr(c)
print d
print d.encode("hex")
The decrypted string ends in "01", a single byte of padding. It's not printable, so it can't be seen in the ASCII version, but it's visible in the hexadecimal version, as highlighted in the image below.

Observing the Padding Oracle Vulnerability

Enter these commands to modify the ciphertext and decrypt the modified ciphertext, as shown below. 
mod = c[0:47] + chr(65)
decr(mod)
Enter this command decrypt the original ciphertext, as shown below. 
decr(c)
As shown below, an error message appears when the padding is incorrect, but not when it is correct.

This seemingly harmless error message is enough to completely defeat the encryption, because it can be used to leak out information about the encryption process.

Problem Statement

Your goal is to create a valid encrypted message including this word: 
WIN
You need to encrypt it with AES-CBC, but you don't know the IV or the key.

You have a single example of encrypted text, and a system that will let you test encrypted text and tell you whether the padding is correct or not.

This should be impossible, but it can be done using the padding oracle attack.

Goal: Intermediate State

Consider the intermediate state shown in the figure below, with one block colored orange. This 16-byte value, intermediate[32:48], depends only on the key and the third block of ciphertext.

If we can figure out the intermediate state, we can create ciphertext that decrypts to any plaintext we want in the third block. We do that by modifying the second block.

We don't need to know the key or the iv.

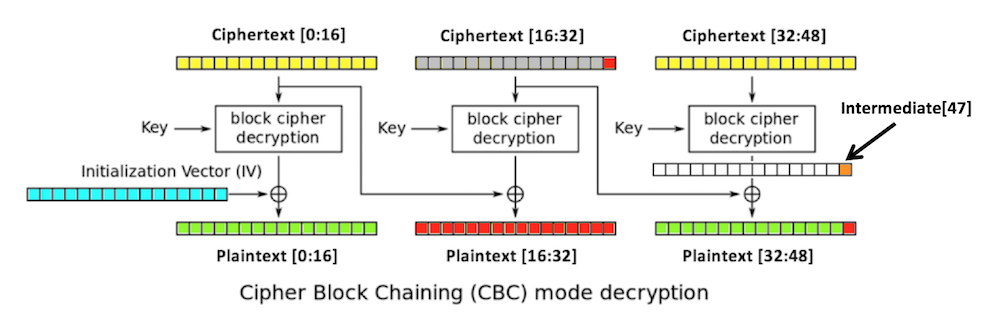
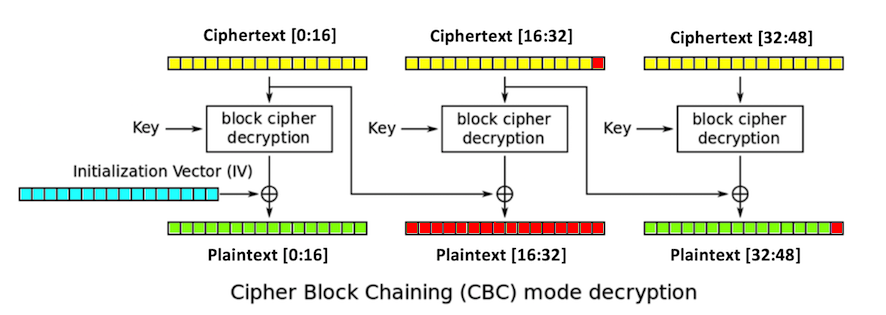
Performing a Padding Oracle Attack

Here's how we can find the last byte of the intermediate state.

1. You start with a valid ciphertext string.

2. Replace ciphertext[16:32] with any random bytes. This will change the second and third blocks of plaintext, including the last byte of plaintext, plaintext[47], which is colored red in the figure below.

The padding of the plaintext will now be invalid, unless plaintext[47] is 1. (There's a small chance that it might be valid in other ways, but let's ignore that for now.)

3. Try all possible byte values for ciphertext[31] until a valid padding is found. Now we know that plaintext[47] is 1.

4. The last intermediate byte is the XOR of those values:

ciphertext[31] ^ 1

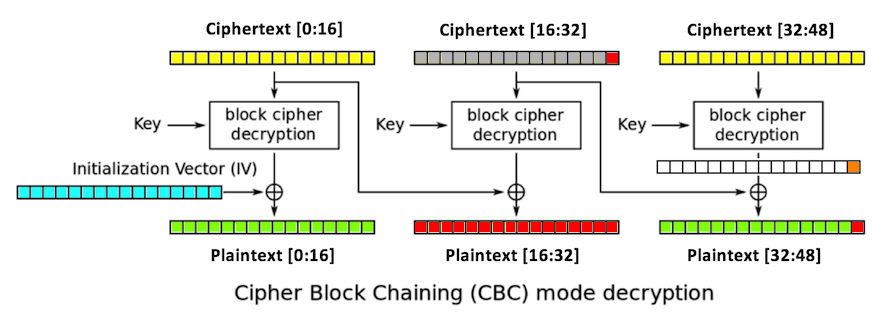
After 256 guesses, we get one byte of the intermediate value. We can continue in this fashion until we get them all, except for the first block.

Getting a Valid Ciphertext

In your Python session, execute these commands to encrypt a sentence containing "I'M A LOSER", and place the value in a variable named "original". 
a = "This sentence cleaarly says I'M A LOSER."
original = encr(a)
print original.encode("hex")
As shown below, the ciphertext is a string of 48 random bytes.

Now we are ready to perform the attack in four stages, as detailed below.

Stage 1. Finding Intermediate[47]

Performing 5 Modifications

In your Python session, execute these commands to try five values for ciphertext[31]. Press Enter twice after the last line of text. 
for i in range(5):
  mod = original[0:31] + chr(i) + original[32:]
  print i, decr(mod)
As shown below, all the modifications result in "PADDING ERROR" messages.

Finding Valid Values

In your Python session, execute these commands to try all 256 possible values for ciphertext[31]. Press Enter twice after the last line of text. 
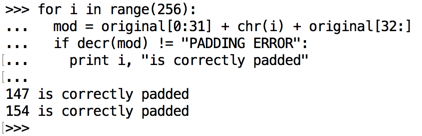
for i in range(256):
  mod = original[0:31] + chr(i) + original[32:]
  if decr(mod) != "PADDING ERROR":
    print i, "is correctly padded"
As shown below, there are two valid values.

One of these is the original byte, which results in a correct string of padding bytes, and the other one results in a final byte of 1, which is interpreted as a correct padding string one byte long.

Execute this command to see the original value of ciphertext[31]. 

print ord(original[31])
As shown below, the original byte is 154. So the other value, 147, must result in a plaintext[47] value of 1.

This was effective, but it would be better to find the value directly, instead of finding two possibilities and needing to choose between them.

Filling Ciphertext[16:31] with "A"

In your Python session, execute these commands to fill the 15 bytes from c[16] through c[31] with "A" characters, and then test all 256 possible values for ciphertext[31]. Press Enter twice after the last line of text. 
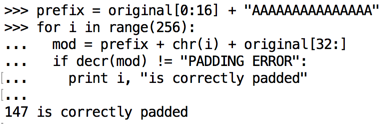
prefix = original[0:16] + "AAAAAAAAAAAAAAA"
for i in range(256):
  mod = prefix + chr(i) + original[32:]
  if decr(mod) != "PADDING ERROR":
    print i, "is correctly padded"
As shown below, the correct value of 147 is found. This worked because the modified ciphertext creates random bytes of cleartext, which won't end in valid padding unless the final byte is 1.

Filling Ciphertext[16:31] with "B"

In your Python session, execute these commands to fill the 15 bytes from c[16] through c[31] with "B" characters, and then test all 256 possible values for ciphertext[31]. Press Enter twice after the last line of text. 
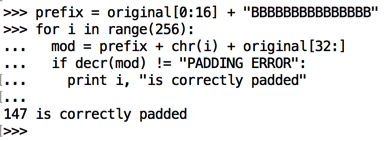
prefix = original[0:16] + "BBBBBBBBBBBBBBB"
for i in range(256):
  mod = prefix + chr(i) + original[32:]
  if decr(mod) != "PADDING ERROR":
    print i, "is correctly padded"
As shown below, the correct value of 147 is found. Almost any values can be used to fill ciphertext[16:31] and the attack will work.

Calculating Intermediate[47]

From the diagram below, we can see that this is how the last byte of the cleartext is calculated:
ciphertext[31] ^ intermediate[47] = plaintext[47]

Applying ciphertext[31] ^ to both sides of this equation yields:

ciphertext[31] ^ ciphertext[31] ^ intermediate[47] = ciphertext[31] ^ plaintext[47]
Rearranging terms yields:
intermediate[47] ^ ciphertext[31] ^ ciphertext[31] = ciphertext[31] ^ plaintext[47]
On the left side, intermediate[47] is XORed with a byte, and then XORed again with the same byte. XOR is its own inverse--XORing twice with the same byte gets you back where you started, so:
intermediate[47] = ciphertext[31] ^ plaintext[47]
And we know that plaintext[47] must be 1 to make the padding valid, so, when the padding is valid,
intermediate[47] = ciphertext[31] ^ 1 = 147 ^ 1 = 146
So now we know this:
intermediate[47] = 146

Stage 2. Finding Intermediate[46]

To find intermediate[46], we can't use the situation with a single padding byte of 1. Instead, we need to set up a situation with two padding bytes of 2 at the end, plaintext[46] and plaintext[47], as shown below.

Making plaintext[47] Equal 2

We know these two values:
intermediate[47] = 146

plaintext[47] = 2

So we need to use this value of ciphertext[31]:
ciphertext[31] = 146 ^ 2 = 144

Trying All Values for ciphertext[30]

In your Python session, execute these commands to fill the 14 bytes from c[16] through c[29] with "B" characters, and then test all 256 possible values for ciphertext[30], using 144 for ciphertext[31]. Press Enter twice after the last line of text. 
prefix = original[0:16] + "BBBBBBBBBBBBBB"
for i in range(256):
  mod = prefix + chr(i) + chr(144) + original[32:]
  if decr(mod) != "PADDING ERROR":
    print i, "is correctly padded"
As shown below, the answer is 6.

Calculating Intermediate[46]

We know that when ciphertext[30]=6, plaintext[46]=2 (required to make the padding valid).

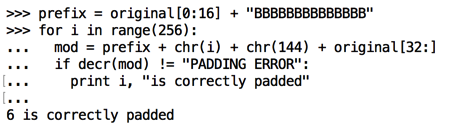
We can now calculate Intermediate[46]

intermediate[46] = ciphertext[30] ^ plaintext[46] = 6 ^ 2 = 4
So now we know this:
intermediate[46] = 4
intermediate[47] = 146

Stage 3. Finding Intermediate[45]

To find intermediate[45], we need to set up a situation with three padding bytes of 3 at the end, plaintext[45], plaintext[46], and plaintext[47].

Making plaintext[46] and plaintext[47] Equal 3

We know these values:
intermediate[46] = 4
intermediate[47] = 146

plaintext[46] = 3
plaintext[47] = 3

So we need to use these values for ciphertext[30] and ciphertext[31]:
ciphertext[30] = 4 ^ 3 = 7
ciphertext[31] = 146 ^ 3 = 145

Trying All Values for ciphertext[29]

In your Python session, execute these commands to fill the 13 bytes from c[16] through c[28] with "B" characters, and then test all 256 possible values for ciphertext[29], using the values found above for ciphertext[30] and ciphertext[31].

Press Enter twice after the last line of text. 

prefix = original[0:16] + "BBBBBBBBBBBBB"
for i in range(256):
  mod = prefix + chr(i) + chr(7) + chr(145) + original[32:]
  if decr(mod) != "PADDING ERROR":
    print i, "is correctly padded"
As shown below, the answer is 102.

Calculating Intermediate[45]

We know that when ciphertext[29]=102, plaintext[45]=3 (required to make the padding valid).

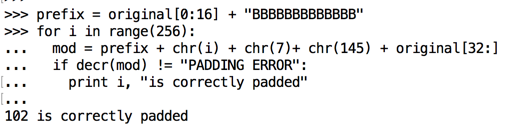
We can now calculate Intermediate[45]

intermediate[45] = ciphertext[29] ^ plaintext[45] = 102 ^ 3 = 101
So now we know this:
intermediate[45] = 101
intermediate[46] = 4
intermediate[47] = 146

Stage 4. Finding Intermediate[44]

To find intermediate[44], we need to set up a situation with four padding bytes of 4 at the end, plaintext[44], plaintext[45], plaintext[46], and plaintext[47].

Making plaintext[45], plaintext[46], and plaintext[47] Equal 4

We know these values:
intermediate[45] = 101
intermediate[46] = 4
intermediate[47] = 146

plaintext[45] = 4
plaintext[46] = 4
plaintext[47] = 4

So we need to use these values for ciphertext[29], ciphertext[30], and ciphertext[31]:
ciphertext[29] = 101 ^ 4 = 97
ciphertext[30] = 4 ^ 4 = 0
ciphertext[31] = 146 ^ 4 = 150

Trying All Values for ciphertext[28]

In your Python session, execute these commands to fill the 12 bytes from c[16] through c[27] with "B" characters, and then test all 256 possible values for ciphertext[28], using the values found above for ciphertext[29], ciphertext[30] and ciphertext[31].

Press Enter twice after the last line of text. 

prefix = original[0:16] + "BBBBBBBBBBBB"
for i in range(256):
  mod = prefix + chr(i) + chr(97) + chr(0) + chr(150) + original[32:]
  if decr(mod) != "PADDING ERROR":
    print i, "is correctly padded"
As shown below, the answer is 235.

Calculating Intermediate[44]

We know that when ciphertext[28]=235, plaintext[45]=4 (required to make the padding valid).

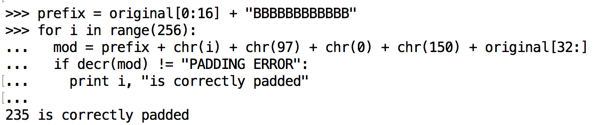
We can now calculate Intermediate[44]

intermediate[44] = ciphertext[28] ^ plaintext[44] = 235 ^ 4 = 239
So now we know this:
intermediate[44] = 239
intermediate[45] = 101
intermediate[46] = 4
intermediate[47] = 146

Stage 5: Encoding WIN

We know this:
intermediate[44] = 239
intermediate[45] = 101
intermediate[46] = 4
intermediate[47] = 146
We want this plaintext, ending with "WIN" and a correct single byte of 1 for padding:
cleartext[44] = ord("W")
cleartext[45] = ord("I")
cleartext[46] = ord("N")
cleartext[47] = 1
So we choose these ciphertext bytes:
ciphertext[28] = cleartext[44] ^ intermediate[44] = ord("W") ^ 239
ciphertext[29] = cleartext[45] ^ intermediate[45] = ord("I") ^ 101
ciphertext[30] = cleartext[46] ^ intermediate[46] = ord("N") ^ 4
ciphertext[31] = cleartext[47] ^ intermediate[47] = 1 ^ 146
Execute these commands to calculate and insert those bytes (it's a little clumsy because Python doesn't let you assign a byte inside a string):
c28 = ord("W") ^ 239
c29 = ord("I") ^ 101
c30 = ord("N") ^ 4
c31 = 1 ^ 146

ciphertext = original[0:28] + chr(c28) + chr(c29) + chr(c30) + chr(c31) + original[32:]

Decrypting the New Ciphertext

Execute this command to decrypt your crafted cypertext. It should end with "WIN", as shown below.
decr(ciphertext)

Saving a Screen Image (Image 14A)

Make sure you can see WIN, as shown above.

Capture a full-screen image.

YOU MUST SUBMIT A FULL-SCREEN IMAGE FOR FULL CREDIT!

Save the image with the filename "YOUR NAME Proj 14a", replacing "YOUR NAME" with your real name.

Challenge: Winners Board (20 pts. extra credit)

Setup

Right-click on the link below, and save the file in your Downloads folder:

padorchal1.pyx

Open a Terminal window and execute these commands: 

cd Downloads
mv padorchal1.pyx padorchal1.py
python
In the Python shell, execute these commands: 
from padorchal1 import decr
a = "3ceafc6720f418f86b937a14fa0703df352b04f7d1e6a1e3bdd2e6f36e3da543800a6b07b3db36b372e934dfeeb2d920"
decr(a)

c="aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
decr(c)
The first string should return 'Error: no name included ', and the second one should return 'PADDING ERROR ', as shown below.

This ciphertext is valid:

3ceafc6720f418f86b937a14fa0703df352b04f7d1e6a1e3bdd2e6f36e3da543800a6b07b3db36b372e934dfeeb2d920
It decodes to this string:
Put this name on the winners board: EXAMPLE
It gives an error message because a name cannot begin with a space.

To get on the winners board, send ciphertext in hex that decodes to a string ending in :YOURNAME with correct padding.

Use the form below to put your name on the WINNERS PAGE.

Ciphertext like this:

3ceafc6720f418f86b937a14fa0703df352b04f7d1e6a1e3bdd2e6f36e3da543800a6b07b3db36b372e934dfeeb2d920

Saving a Screen Image (Image 14B)

Save a whole-screen image of the winners page showing your name, as shown below, with the filename "YOUR NAME Proj 14b".

Turning in your Project

Email the images to cnit.141@gmail.com with the subject line: Proj 14 from YOUR NAME.

Sources

The Padding Oracle Attack - why crypto is terrifying
Block cipher mode of operation - Wikipedia
PKCS #7: Cryptographic Message Syntax (section 10.3)

Posted 10-19-17 5:26 am by Sam Bowne
Hex example added to form 11-18-17