C 800: Baby Kyber (40 pts extra)

What You Need

Any machine with Python 3 and openssl. I used Google Colab.

Purpose

To learn how CRYSTALS-KYBER works, a lattice cryptography system approved by NIST for key agreement over an untrusted communications channel. This system will replace Diffie-Hellman methods using RSA and ECC.

We will use a scaled-down version of Kyber called Baby Kyber, following this page:

Kyber - How does it work?

Key Generation

To generate the keys, we need these quantities:
s: a vector of polynomials with random small coefficients -- this is the private key  
q: a modulus for coefficients  
f: a modulus for polynomials, set to x4 + 1
A: a matrix of random polynomials  
e: a vector of small random error values  
t: a calculated vector of polynomials

The public key is (A, t)

Private Key Generation

In Kyber, the private key consists of the coefficients for a set of polynomials. The coefficients are random and small. In Baby Kyber, the private key consists of two polynomials:
s = ( -x3 -x2 +x, -x3 -x)

Public Key Generation

We need a modulus, called q. For Baby Kyber, we'll use:
q = 17
Next, we generate a matrix of random polynomials, called called A. The coefficients are taken modulus q.
A = [ 
6x3 +16x2 +16x + 11     9x3 +4x2 +6x + 3
5x3 +3x2 +10x + 1     6x3 +x2 +9x + 15
 ]
We'll use these errors:
e = ( x2, x2 -x)
Now we calculate t by matrix multiplication and addition:
t = As + e
t = [ 
6x3 +16x2 +16x + 11     9x3 +4x2 +6x + 3
5x3 +3x2 +10x + 1     6x3 +x2 +9x + 15
 ] [ 
-x3 -x2 +x
-x3 -x
 ]   +   [ 
x2
x2 -x
 ]
Calculating the top term of t:
( 6x3 +16x2 +16x + 11 ) ( -x3 -x2 +x )  +   ( 9x3 +4x2 +6x + 3 ) ( -x3 -x )   +  x2  =


-6x6   -6x5  +6x4
-16x5   -16x4   +16x3
-16x4   -16x3   +16x2
-11x3   -11x2   +11x
-9x6   -9x4
-4x5   -4x3
-6x4   -6x2
-3x3   -3x
+x2

=
 
-15x6 -26x5 -41x4 -18x3 +8x
All polynomials are calculated modulus f = x4 + 1, so we can replace all occurrences of x4 with -1, giving:
15x2   +26x   +41   -18x3   +8x   =   -18x3 +15x2 +34x + 41
Finally, we take all polynomial coefficients modulus q = 17, giving:
16x3 +15x2 + 7
Calculating the bottom term of t:
( 5x3 +3x2 +10x + 1 ) ( -x3 -x2 +x )  +   ( 6x3 +x2 +9x + 15 ) ( -x3 -x )   +  x2 -x  =


-5x6   -5x5  +5x4
-3x5   -3x4   +3x3
-10x4   -10x3   +10x2
-x3   -x2   +x
-6x6   -6x4
-x5   -x3
-9x4   -9x2
-15x3   -15x
+x2
   -x

=
 
-11x6 -9x5 -23x4 -24x3 +x2 -15x
All polynomials are calculated modulus f = x4 + 1, so we can replace all occurrences of x4 with -1, giving:
11x2   +9x   +23   -24x3   +x2   -15x   =   -24x3 +12x2 -6x + 23
Finally, we take all polynomial coefficients modulus q = 17, giving:
10x3 +12x2 +11x + 6
The final result is:
t = [ 
16x3 +15x2 + 7
10x3 +12x2 +11x + 6
 ]

Public and Private Keys

So the final results are:

Private key:    s = ( -x3 -x2 +x, -x3 -x)

Public key:    (A, t), where

A = [ 
6x3 +16x2 +16x + 11     9x3 +4x2 +6x + 3
5x3 +3x2 +10x + 1     6x3 +x2 +9x + 15
 ]
t = ( 16x3 +15x2 + 7, 10x3 +12x2 +11x + 6)

C 800.1: Public Key (10 pts)

Use the values below to calculate t:
A = [ 
x3 +4x2 + 1     3x3 +12x2 +14x + 5
3x3 +12x2 +2x     11x3 +4x2 +2x + 5
 ]
s = ( x3 -x, -x3 -x2 -x)

e = ( x3 +x2 +x, -x2 -x)

To construct the flag, append all the non-zero coefficients, as shown below.

If t were:

t = ( 16x3 +15x2 + 7, 10x3 +12x2 +11x + 6)
The key would be 161571012116.

Kyber in Python

Performing these calculations by hand is difficult, even for Baby Kyber, and obviously will be impossible for real full-scale Kyber, with much larger polynomials, vectors, and matrices.

So we'll use a simple set of Python functions from this page:

Adventures in PQC: Exploring Kyber in Python - Part I

Calculating a Public Key with Python

In Google Colab, execute these commands. Note: if you are not using Colab, execute the commands starting with ! in a Bash shell.

Notice that polynomial coefficients are in reverse order, starting with x0, then x1, then x2, etc. 

!wget https://samsclass.info/141/proj/kyber.pyx
!mv kyber.pyx kyber.py

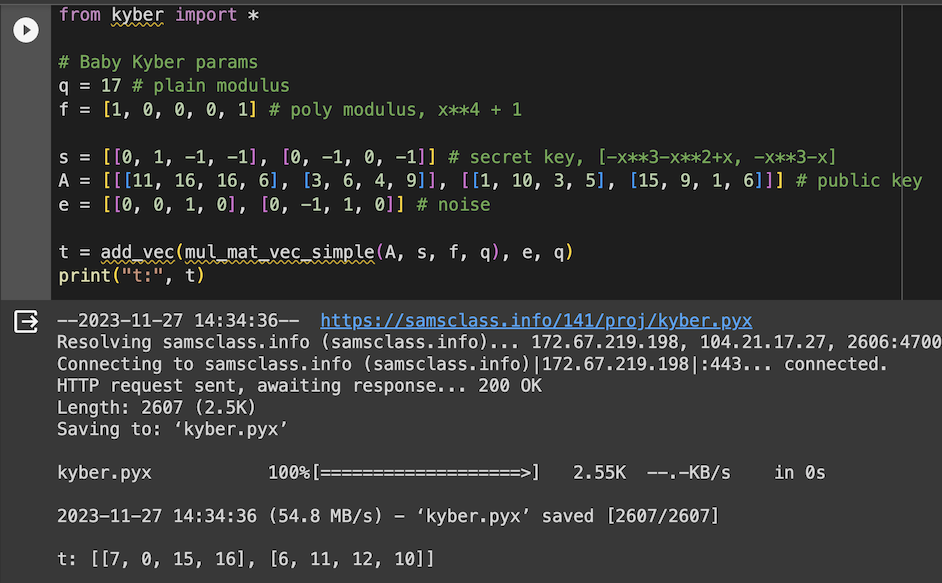
from kyber import *

# Baby Kyber params
q = 17 # plain modulus
f = [1, 0, 0, 0, 1] # poly modulus, x**4 + 1

s = [[0, 1, -1, -1], [0, -1, 0, -1]] # secret key, [-x**3-x**2+x, -x**3-x]
A = [[[11, 16, 16, 6], [3, 6, 4, 9]], [[1, 10, 3, 5], [15, 9, 1, 6]]]
e = [[0, 0, 1, 0], [0, -1, 1, 0]] # noise

t = add_vec(mul_mat_vec_simple(A, s, f, q), e, q)
print("t:", t)
As shown below, it calculates t correctly.

Again, notice that the order of the coefficients is reversed in this Python implementation,

C 800.2: Public Key (10 pts)

Use the values below to calculate t:
A = [ 
6x3 +1x2 + 13x + 3     9x3 +2x2 +11x + 16
9x3 +5x2 +5x + 10     9x3 +8x2 +7x + 6
 ]
s = ( -x3 +x2 +x, x3 -x2 +x)

e = ( -x3 -x, x3 -x2)

q = 17

To construct the flag, append all the non-zero coefficients, as shown below.

If t were:

t = ( 16x3 +15x2 + 7, 10x3 +12x2 +11x + 6)
The key would be 161571012116.

Encryption and Decryption

To encrypt, we need these quantities:
A randomizer polynomial vector r with random small coefficients
An error polynomial vector e1 with random small coefficients
An error polynomial e2 with random small coefficients
A message composed of four bits
For this example, we'll use:
r = ( -x3 +x2, x3 +x2 -1)

e1 = ( x2 +x, x2)

e2 = -x3 -x2

message = 1011

We encode the message, using the bits as coefficients for a polynomial:
Encoded message (1011)  =   1x3 +0x2 +1x +1  =   x3 +x +1
To make the message large enough to overcome the errors, we scale it by multiplying by half the modulus q, rounded up, which is 9 for our example.

The final scaled encoded message is:

m   =   9x3 +9x +9
The encryption process is:
u   =   ATr + e1

v   =   tTr + e2 +m

Errors are added, so the answer is different each time.

Decryption uses this formula:

mn   =   v - sTu
The result is noisy because of the errors. This is why each coefficient encodes only one bit, despite having values from 0 to 16.

To complete the decryption process, coefficients correspond to bits like this:

In Google Colab, execute these commands. 
# Baby Kyber params
q = 17 # plain modulus
f = [1, 0, 0, 0, 1] # poly modulus, x**4 + 1

s = [[0, 1, -1, -1], [0, -1, 0, -1]] # secret key, [-x**3-x**2+x, -x**3-x]
A = [[[11, 16, 16, 6], [3, 6, 4, 9]], [[1, 10, 3, 5], [15, 9, 1, 6]]]
e = [[0, 0, 1, 0], [0, -1, 1, 0]] # noise

t = add_vec(mul_mat_vec_simple(A, s, f, q), e, q)

m_b = [1, 1, 0, 1] # message in binary

r = [[0, 0, 1, -1], [-1, 0, 1, 1]] # blinding vector for encrypt
e_1 = [[0, 1, 1, 0], [0, 0, 1, 0]] # noise vector for encrypt
e_2 = [0, 0, -1, -1] # noise poly for encrypt

u, v = encrypt(A, t, m_b, f, q, r, e_1, e_2)
print("Encrypted message (u, v):", u, v)

m_b2 = decrypt(s, u, v, f, q)
print("Decrypted message:", m_b2)
As shown below, encryption produces random-appearing numbers, but they decrypt to the correct message.

C 800.3: Encryption (10 pts)

Use the values below to calculate t:
A = [ 
6x3 +1x2 + 13x + 3     9x3 +2x2 +11x + 16
9x3 +5x2 +5x + 10     9x3 +8x2 +7x + 6
 ]
s = ( -x3 +x2 +x, x3 -x2 +x)

e = ( -x3 -x, x3 -x2)

q = 17

r = ( -x3 -x2, x3 -x2 -1)

e1 = ( -x2 +x, -x2)

e2 = x3 +x2

message = 1010

To construct the flag, concatenate all the non-zero coefficients covered by a green rectangle in the image below.

This will form a seven-digit number.

Decryption

To decrypt, we need these quantities:
A private key s
An encrypted message (u, v)
We'll also use the coefficient modulus q and the polynomial modulus f, at the same values used above. For this example, we'll use:
s = ( -x3 -x2 +x, -x3 -x)
Here's the encrypted message we created above, in our Python format: 
u, v = [[3, 10, 11, 11], [11, 13, 4, 4]], [15, 8, 6, 7]
To perform the decryption, in Google Colab, execute these commands. 
q = 17 
f = [1, 0, 0, 0, 1] 
s = [[0, 1, -1, -1], [0, -1, 0, -1]] 
u, v = [[3, 10, 11, 11], [11, 13, 4, 4]], [15, 8, 6, 7]
m_b2 = decrypt(s, u, v, f, q)
print("Decrypted message:", m_b2)
As shown below, the message decrypts to the correct value of 1011, with the bits in reverse order.

C 800.4: Decryption (10 pts)

Use the values below to calculate t:
s = ( x2 +1, x3 +x2 +x +1)

Encrypted message (u, v): [[3, 15, 5, 2], [6, 4, 6, 9]] [15, 8, 11, 6]

The flag is the decrypted message as a four-bit binary number, like 1011

Sources

NIST: Post-Quantum Cryptography PQC
FIPS 203 (Initial Public Draft) Module-Lattice-Based Key-Encapsulation Mechanism Standard
Kyber - How does it work?
Adventures in PQC: Exploring Kyber in Python - Part I

Posted 11-27-23 by Sam Bowne
Flag 1 values restored 12-10-23