C 524: Elliptic Curves and Schnorr Signatures (75 pts extra)

What you need:

Purpose

To practice using Elliptic Curves as they are used in Elliptic Curve Cryptography.

Background

A Point is defined by its x and y coordinates, which are both integers.

Each elliptic curve we'll use is defined by the two parameters a and b in the equation below.

y 2 = x 3 + ax + b mod p
All calculations are made modulus p. p is a prime number.

1: Finding Points on the Curve

Downloading the ECC Library and Installing Numpy

I'm using a Python library adapted from this tutorial. It uses the Numpy library.

On your Mac or Linux machine, in a Terminal window, execute these commands: 

wget https://gist.githubusercontent.com/sambowne/d8a3984f3ee987facae1133afee55648/raw/64306798a03a5340dc30889622c629416895debf/ecc.py

python3 -m pip install numpy

A Very Minimal Examnple

Consider this curve:
y 2 = x 3 + x + 2
Consider the case x = -1. All the terms on the right side cancel out, so
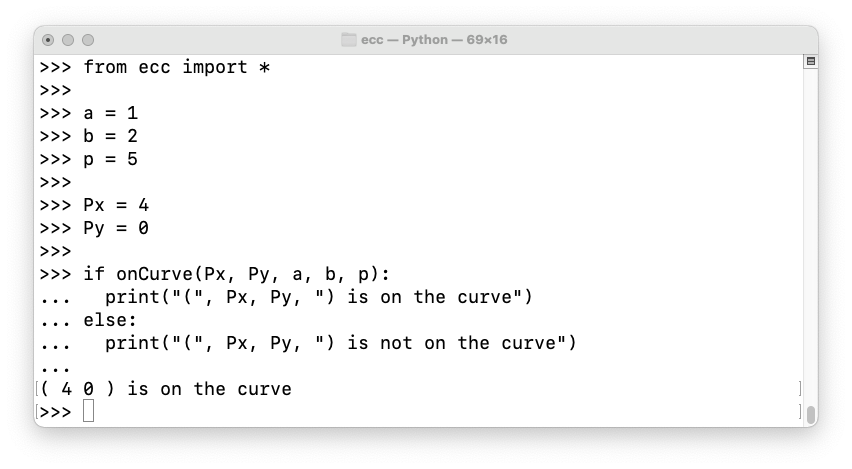
y 2 = 0
One solution is (x, y) = (-1, 0), which we can also write as (4, 0) (mod 5).

We can say the Point (4, 0) is on the curve.

We can determine whether a point is on the curve using the onCurve() function.

On your Mac or Linux machine, in a Terminal window, execute the commands below. Press Enter twice after the last command. 

python3

from ecc import *

a = 1
b = 2
p = 5

Px = 4
Py = 0

if onCurve(Px, Py, a, b, p):
  print("(", Px, Py, ") is on the curve")
else:
  print("(", Px, Py, ") is not on the curve")
The point (4, 0) is on the curve, as shown below.

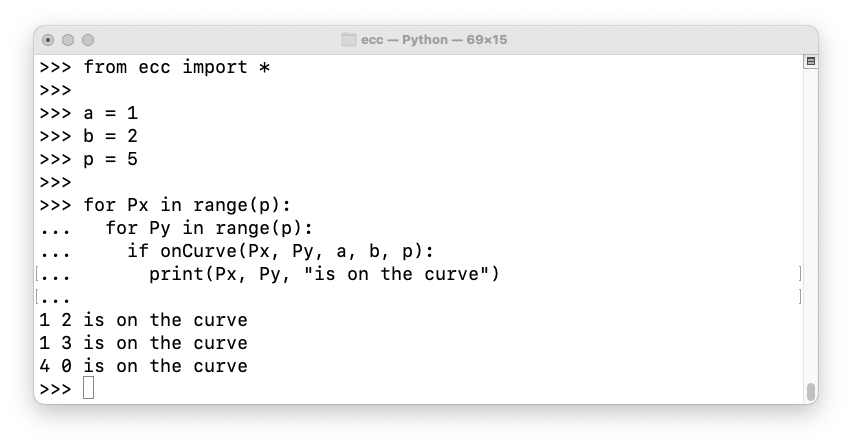
Let's find all the points on the curve.

On your Mac or Linux machine, in a Terminal window, execute the commands below. Press Enter twice after the last command. 

from ecc import *

a = 1
b = 2
p = 5

for Px in range(p):
  for Py in range(p):
    if onCurve(Px, Py, a, b, p):
      print(Px, Py, "is on the curve")
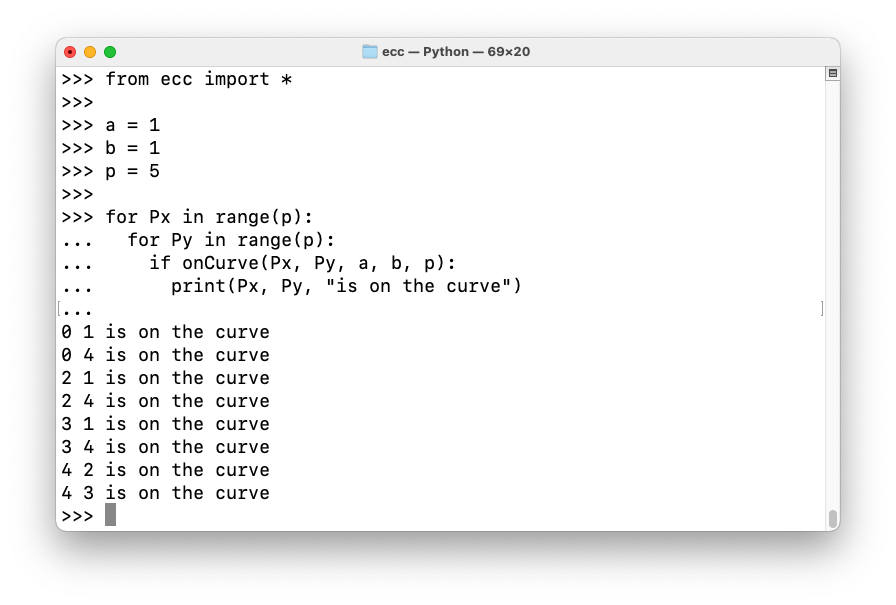
There are three points on the curve, as shown below. There's also a point at infinity, bringing the total to 4. This number is called the order of the curve and denoted by n.

Let's change b to 1.

On your Mac or Linux machine, in a Terminal window, execute the commands below. Press Enter twice after the last command.

Now there are eight points on the curve (plus the point at infinity), as shown below.

The number of points on an elliptic curve varies, but it's never very far away from p, as explained here.

C 524.1: Secp256k1 (5 pts)

This is the curve used by Bitcoin, (with a higher p):
  • a = 0
  • b = 7
  • p = 11
How many points are on this curve, not including the point at infinity? That number is the flag.

C 524.2: Secp256k1 with Larger p (10 pts)

Use this curve:
  • a = 0
  • b = 7
  • p = 6199
What is the largest y of any point on the curve, excluding the point at infinity? That number is the flag.

2. Scalar Multiplication

The ecc library we're using has this function, which multiplies a point P by an integer k:
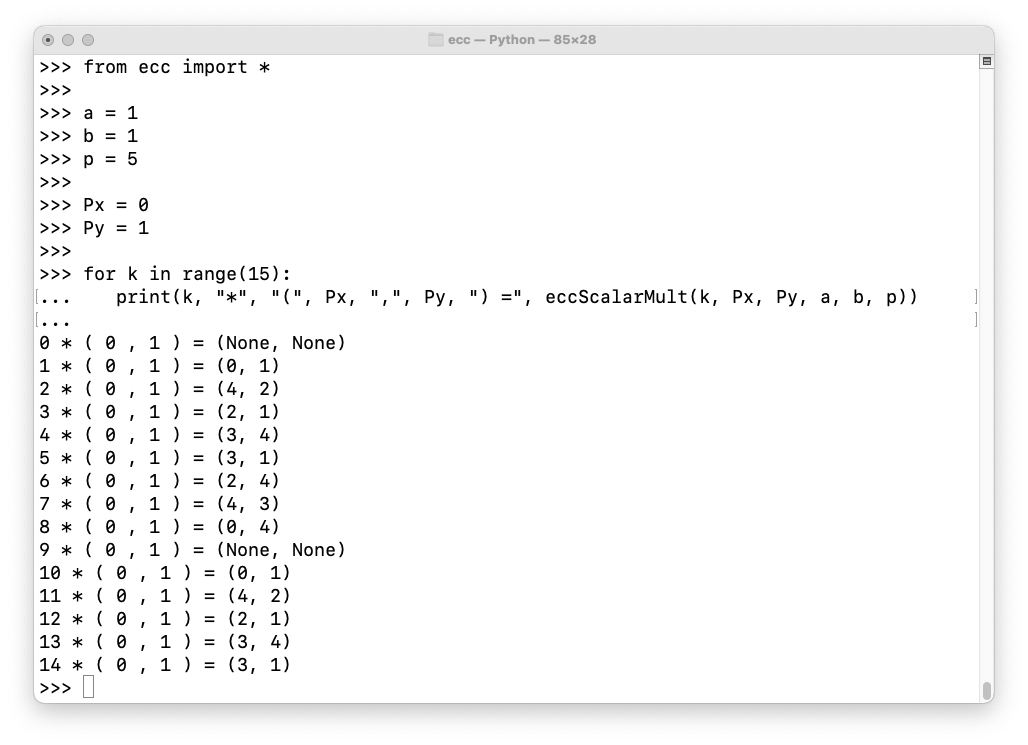
eccScalarMult(k, Px, Py, a, b, p)
As we saw before, here are the points on this curve:

Execute these commands to see various multiples of (0, 1): 

from ecc import *

a = 1
b = 1
p = 5

Px = 0
Py = 1

for k in range(15):
   print(k, "*", "(", Px, ",", Py, ") =", eccScalarMult(k, Px, Py, a, b, p))
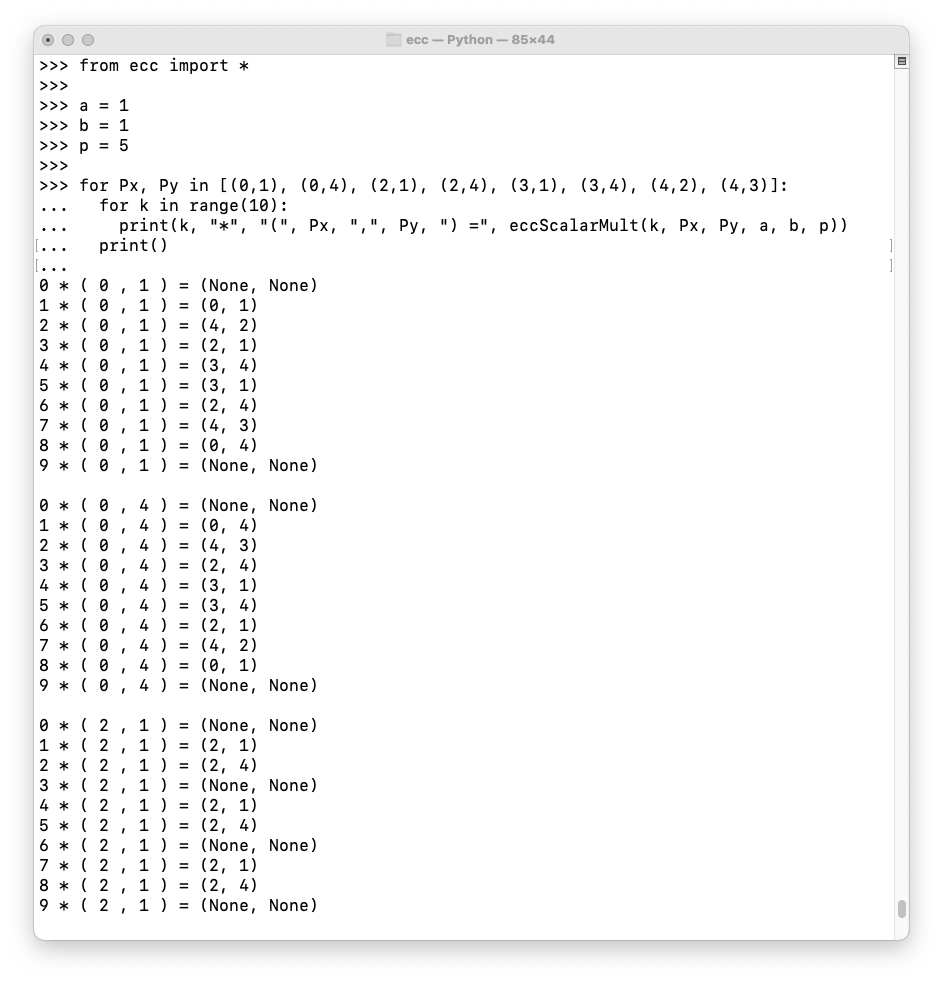
All eight points are generated, as shown below, as well as (None, None), the "point at infinity". (0, 1) is a generator of the curve.

Execute these commands to list multiples of all eight points on the curve: 

from ecc import *

a = 1
b = 1
p = 5

for Px, Py in [(0,1), (0,4), (2,1), (2,4), (3,1), (3,4), (4,2), (4,3)]:
  for k in range(10):
    print(k, "*", "(", Px, ",", Py, ") =", eccScalarMult(k, Px, Py, a, b, p))
  print()
As shown below, (2, 1) is not a generator of the curve:

C 524.3: Generators (5 pts)

Use the curve defined below:
  • a = 2
  • b = 3
  • p = 7
How many points on this curve are generators? That number is the flag.

C 524.4: More Generators (10 pts)

Use the curve defined below:
  • a = 2
  • b = 3
  • p = 101
How many points on this curve are generators? That number is the flag.

3. Elliptic-Curve Diffie–Hellman (ECDH)

Consider the Secp256k1 curve with p = 17.

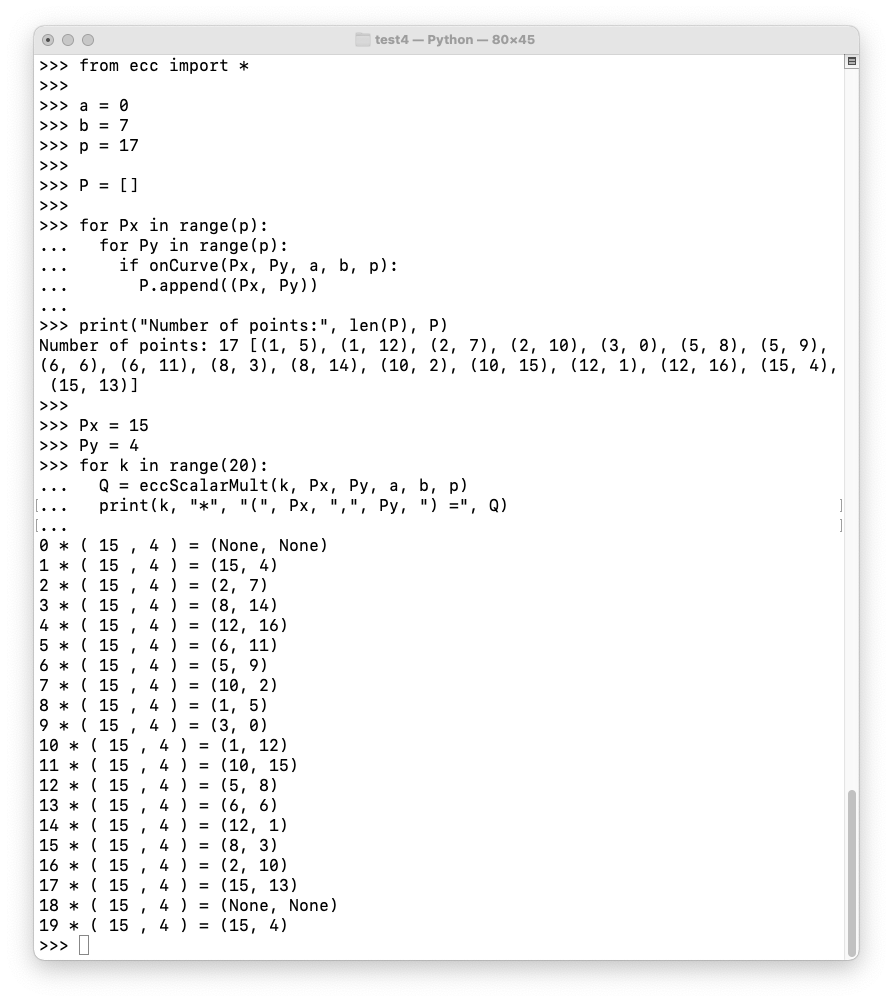
Execute the code below to confirm that there are 17 points on this curve (not including the point at infinity), and that (15, 4) is a generator. 

from ecc import *

a = 0
b = 7
p = 17

P = []

for Px in range(p):
  for Py in range(p):
    if onCurve(Px, Py, a, b, p):
      P.append((Px, Py))

print("Number of points:", len(P), P)

Px = 15
Py = 4
for k in range(20):
  Q = eccScalarMult(k, Px, Py, a, b, p)
  print(k, "*", "(", Px, ",", Py, ") =", Q)

Key Agreement

Cueball and Meghan wish to communicate privately.

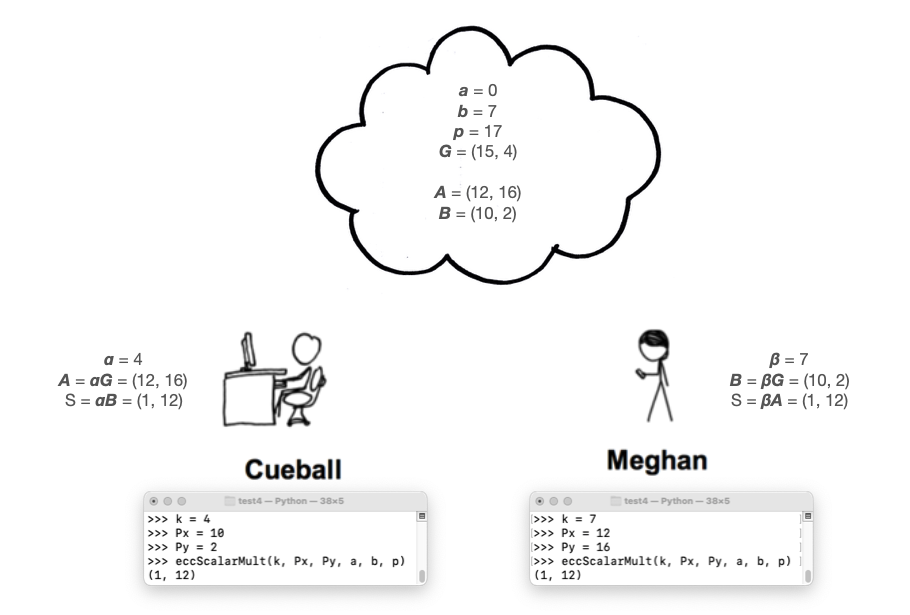
As shown below, they agree on a curve (Secp256k1), p, and a generator G. These parameters are not secret--they can be published to the public cloud.

Cueball picks a random number α, between 1 and p - 1. α is his private key.
Cueball calculates his public key A = αG , and publishes it to the cloud.

Meghan chooses a private key of β, calculates her public key B = βG , and publishes it to the cloud.

Each of them multiplies their private key and the other person's public key to find a Shared Secret, as shown below.

Unlike RSA, ECC does not provide any way to encrypt or decrypt with the public or private keys.

Instead, the Shared Secret can be used to determine an encryption key using PBKDF2 or some other algorithm, and the data can be encrypted with AES.

The Discrete Logarithm Problem

Can an attacker learn the Shared Secret from the public information? Only by deducing one of the private key values, which is the Discrete Logarithm Problem:
Given A, find α such that A = αG
This problem is very difficult if a good elliptic curve is chosen, with a large enough value of p.

C 524.5: ECDH (5 pts)

Use the curve defined below:
  • a = 0
  • b = 7
  • p = 761
  • G = (3, 107)
Cueball 's private key is 94. What is his public key? That's the flag.

C 524.6: DLP (10 pts)

Use the same curve as in the previous challenge.

Megan's public key is (744, 52).

Find her private key. That's the flag.

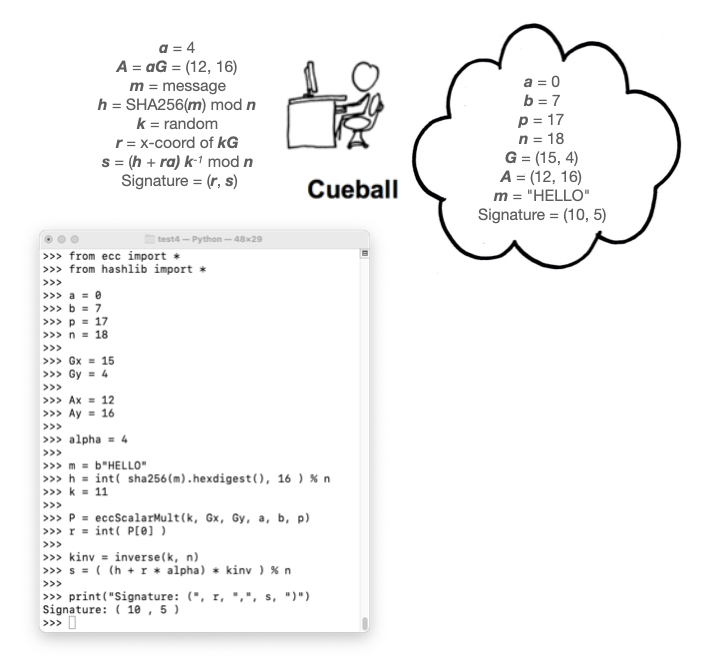
4. Elliptic-Curve Digital Signature Algorithm (ECDSA)

As shown below, both parties agree on a curve and a generator.

Cueball has:

Here's how he creates a signature:
  1. Calculate the hash h of the message m (mod n for this small-number example)
  2. Pick a random number k
  3. Calculate r = the x-coordinate of kG mod n
  4. Calculate signature s = (h + rα) k -1 mod n
  5. Publish the signature as (r, s)

Calculating a Signature

Execute these commands to calculate Cueball's signature: 
from ecc import *
from hashlib import *

a = 0
b = 7
p = 17
n = 18

Gx = 15
Gy = 4

Ax = 12
Ay = 16

alpha = 4

m = b"HELLO"
h = int( sha256(m).hexdigest(), 16 ) % n
k = 11

P = eccScalarMult(k, Gx, Gy, a, b, p)
r = int( P[0] )

kinv = inverse(k, n)
s = ( (h + r * alpha) * kinv ) % n

print("Signature: (", r, ",", s, ")")
The result is (10, 15) as shown in the image above.

Verifying a Signature

Meghan does this to verify the signature:
  1. Calculate w = s -1 mod n
  2. Calculate u = wh
  3. Calculate v = wr
  4. Calculate Q = uG + vA (A is the signer's public key)
  5. The x-coordinate of Q should equal r

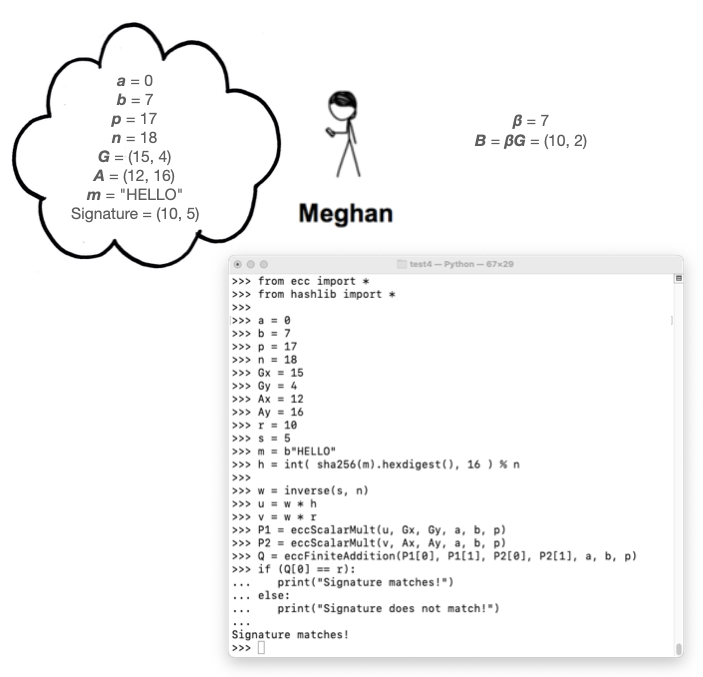
Execute these commands to verify Cueball's signature: 

from ecc import *
from hashlib import *

a = 0
b = 7
p = 17
n = 18
Gx = 15
Gy = 4
Ax = 12
Ay = 16
r = 10
s = 5
m = b"HELLO"
h = int( sha256(m).hexdigest(), 16 ) % n

w = inverse(s, n)
u = w * h
v = w * r
P1 = eccScalarMult(u, Gx, Gy, a, b, p)
P2 = eccScalarMult(v, Ax, Ay, a, b, p)
Q = eccFiniteAddition(P1[0], P1[1], P2[0], P2[1], a, b, p)
if (Q[0] == r):
   print("Signature matches!")
else:
   print("Signature does not match!")
The result is (10, 15) as shown in the image above.

C 524.7: Meghan's ECDSA Signature (5 pts)

Megan wants to sign the same message, "HELLO". As shown in the image above, her private and public keys are: 
β = 7
B = (10, 2)
Use a k of 7, and the same curve as in the figure above.

Calculate Megan's signature. That's the flag.

C 524.8: Validate Meghan's ECDSA Signature (5 pts)

Validate Megan's signature. The flag is the value Q

Schnorr Signatures

This is a method for multiple people to sign the same message, thus consuming less data on the blockchain. It was incorporated into Bitcoin as part of the Taproot update in November 2021.

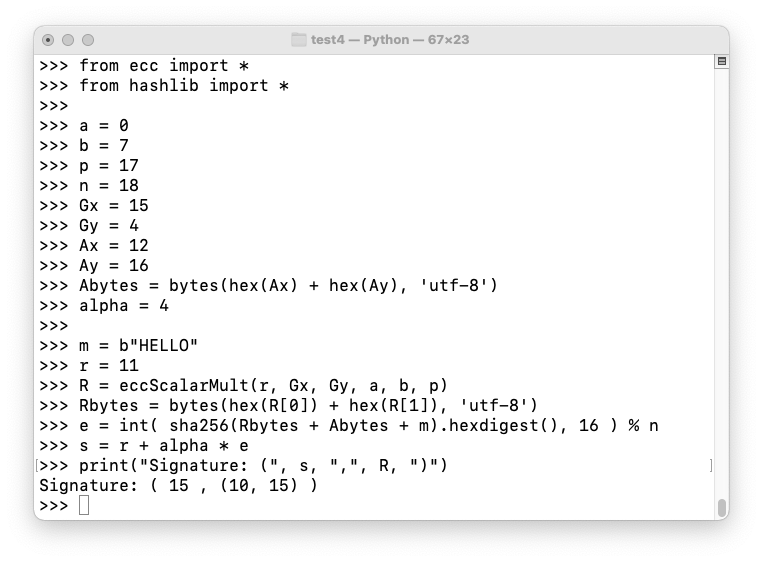
Here's how Cueball creates a signature, as shown in the image below:

  1. Pick a random nonce r
  2. Calculate a public key R = rG
  3. Calculate a challenge e combining all the public information: e = H(R||A||m), where H is a hash function and || indicates concatenation.
  4. Construct the signature using your private information: s = r + αe
  5. Publish (s, R)
To verify the signature:
  1. Calculate c = sG
  2. Calculate e = H(R||A||m)
  3. Calculate d = R + Ae
  4. If c = d, the signature is valid.
Execute these commands to calculate Cueball's signature: 
from ecc import *
from hashlib import *

a = 0
b = 7
p = 17
n = 18
Gx = 15
Gy = 4
Ax = 12
Ay = 16
Abytes = bytes(hex(Ax) + hex(Ay), 'utf-8')
alpha = 4

m = b"HELLO"
r = 11
R = eccScalarMult(r, Gx, Gy, a, b, p)
Rbytes = bytes(hex(R[0]) + hex(R[1]), 'utf-8')
e = int( sha256(Rbytes + Abytes + m).hexdigest(), 16 ) % n
s = r + alpha * e
print("Signature: (", s, ",", R, ")")
The signature is (15, (10, 15)), as shown below.

Execute these commands to verify Cueball's signature: 

from ecc import *
from hashlib import *

a = 0
b = 7
p = 17
n = 18
Gx = 15
Gy = 4
Ax = 12
Ay = 16
Abytes = bytes(hex(Ax) + hex(Ay), 'utf-8')

m = b"HELLO"
R = (10, 15)
Rbytes = bytes(hex(R[0]) + hex(R[1]), 'utf-8')
s = 15
c = eccScalarMult(s, Gx, Gy, a, b, p)
e = int( sha256(Rbytes + Abytes + m).hexdigest(), 16 ) % n
Ae = eccScalarMult(e, Ax, Ay, a, b, p)
d = eccFiniteAddition(R[0], R[1], Ae[0], Ae[1], a, b, p)

if c==d:
  print("Signature is valid!")
else:
  print("Signature is not valid!")
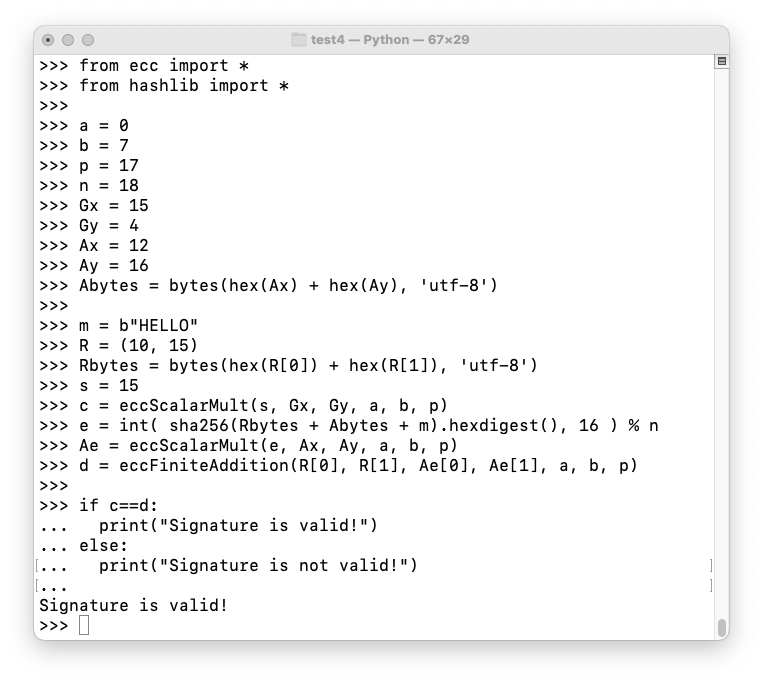
The signature is valid, as shown below.

C 524.9: Meghan's Schnorr Signature (5 pts)

Megan wants to sign the same message, "HELLO". Her private and public keys are: 
β = 7
B = (10, 2)
Use a r of 5, and the same curve as in the figure above.

Calculate Megan's Schnorr signature. That's the flag.

C 524.10: Validate Meghan's Schnorr Signature (5 pts)

Validate the signature you found above. The flag is the d value.

Signature Aggregation

The main advantage of Schnorr signatures is they allow multiple parties to sign a transaction with a single aggregate signature, conserving space on the blockchain.

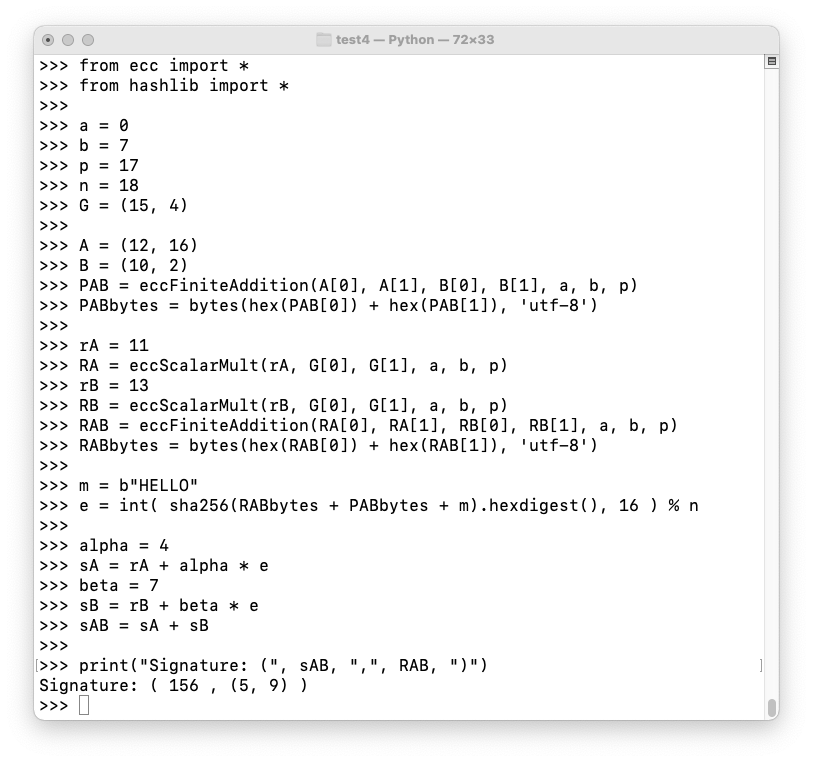
Cueball and Meghan both want to sign a message.

Here's how they do it:

  1. Cueball has a known public key A and Meghan has a known public key B
  2. These are added together to produce the aggregate public key PAB = A + B
  3. Cueball picks a random nonce rA and calculates another public key from it RA = rAG
  4. Meghan picks a random nonce rB and calculates another public key from it RB = rBG
  5. These public keys are added to produce the aggregate public key: RAB = RA + RB
  6. They both calculate the same challenge e combining all the public information: e = H(RAB||PAB||m), where H is a hash function and || indicates concatenation.
  7. Cueball constructs a signature using his private information: sA = rA + αe and publishes it
  8. Methan constructs a signature using her private information: sB = rB + βe and publishes it
  9. The aggregate signature sAB = sA + sB
  10. The aggregate signature is published as (sAB, RAB)
To verify the signature:
  1. Calculate c = sABG
  2. Calculate e = H(RAB||PAB||m))
  3. Calculate d = RAB + PABe
  4. If c = d, the signature is valid.
Execute these commands to calculate the aggregate signature: 
from ecc import *
from hashlib import *

a = 0
b = 7
p = 17
n = 18
G = (15, 4)

A = (12, 16)
B = (10, 2)
PAB = eccFiniteAddition(A[0], A[1], B[0], B[1], a, b, p)
PABbytes = bytes(hex(PAB[0]) + hex(PAB[1]), 'utf-8')

rA = 11
RA = eccScalarMult(rA, G[0], G[1], a, b, p)
rB = 13
RB = eccScalarMult(rB, G[0], G[1], a, b, p)
RAB = eccFiniteAddition(RA[0], RA[1], RB[0], RB[1], a, b, p)
RABbytes = bytes(hex(RAB[0]) + hex(RAB[1]), 'utf-8')

m = b"HELLO"
e = int( sha256(RABbytes + PABbytes + m).hexdigest(), 16 ) % n

alpha = 4
sA = rA + alpha * e
beta = 7
sB = rB + beta * e
sAB = sA + sB

print("Signature: (", sAB, ",", RAB, ")")
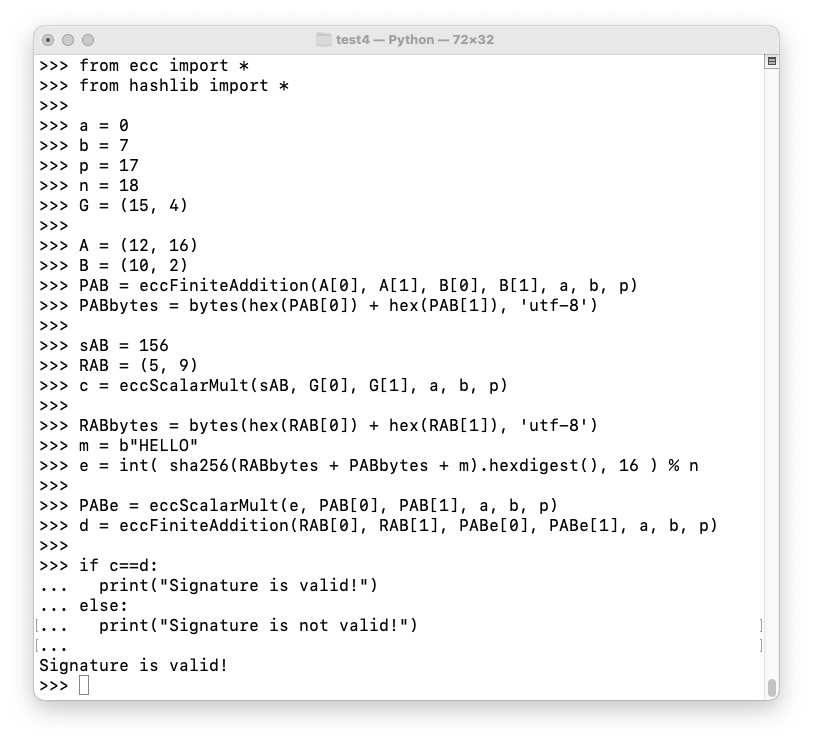
The signature is (156, (5, 9)), as shown below.

Execute these commands to verify the aggregate signature: 

from ecc import *
from hashlib import *

a = 0
b = 7
p = 17
n = 18
G = (15, 4)

A = (12, 16)
B = (10, 2)
PAB = eccFiniteAddition(A[0], A[1], B[0], B[1], a, b, p)
PABbytes = bytes(hex(PAB[0]) + hex(PAB[1]), 'utf-8')

sAB = 156
RAB = (5, 9)
c = eccScalarMult(sAB, G[0], G[1], a, b, p)

RABbytes = bytes(hex(RAB[0]) + hex(RAB[1]), 'utf-8')
m = b"HELLO"
e = int( sha256(RABbytes + PABbytes + m).hexdigest(), 16 ) % n

PABe = eccScalarMult(e, PAB[0], PAB[1], a, b, p)
d = eccFiniteAddition(RAB[0], RAB[1], PABe[0], PABe[1], a, b, p)

if c==d:
  print("Signature is valid!")
else:
  print("Signature is not valid!")
The signature is valid, as shown below.

C 524.11: Aggregate Schnorr Signature (5 pts)

Add Ponytail, shown below, to the aggregate signature above, so there are three signers.

Use an r of 3.

The composite Schnorr signature is the flag.

C 524.12: Validate the Aggregate Schnorr Signature (5 pts)

Validate the signature you found above. The flag is the d value.

References

Elliptic Curve Cryptography and Diffie-Hellman Key Exchange
Elliptic Curve Cryptography (ECC)
Elliptic Curve Calculator
Elliptic Curve scalar multiplication
Schnorr Signature
Introduction to Schnorr Signatures

Posted 11-21-21