C 510: Quantum Computing (20 pts)

What you need

Purpose

To practice using a simulated quantum computer for very basic operations.

Creating a PythonAnywhere Account

The library used here is difficult to install. The easiest way to use it is with a cloud service.

In a Web brower, go to

https://www.pythonanywhere.com/pricing/
Click "Create a Beginner account".

Fill in the form to create an account.

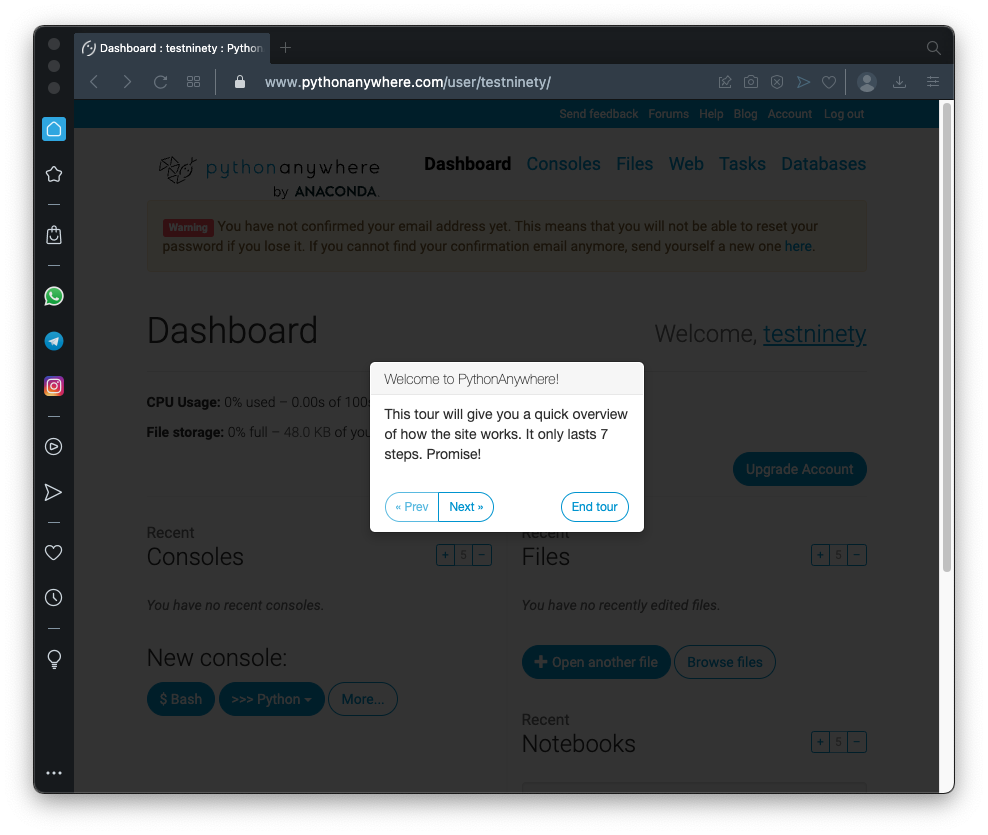
Go through the tour, as shown below.

Using a Bash Console

From the PythonAnywhere Dashboard, on the lower left, in the "New console" section, click the "$ Bash" button, as shown below.

Installing ProjectQ

Execute these commands. 
python3 -m pip install --upgrade pip
python3 -m pip install --user projectq
There are a lot of messages, and the installation succeeds, as shown below.

A Qubit in State |0>

Normal computers use bits, which are always 0 or 1. Quantum computers use qubits, which are more complex than bits. However, qubits can be used to encode bits, as we will do here.

Execute this command to create a file named q1.py 

nano q1.py
Paste in this code, as shown below.

This program creates a qubit and measures it ten times. 

from projectq.ops import Measure
from projectq import MainEngine
quantum_engine = MainEngine()

print("Default Qubit in state |0>", end=" ")
for i in range(10):
   qubit = quantum_engine.allocate_qubit()
   Measure | qubit
   quantum_engine.flush()
   print(int(qubit), end=" ")
print()

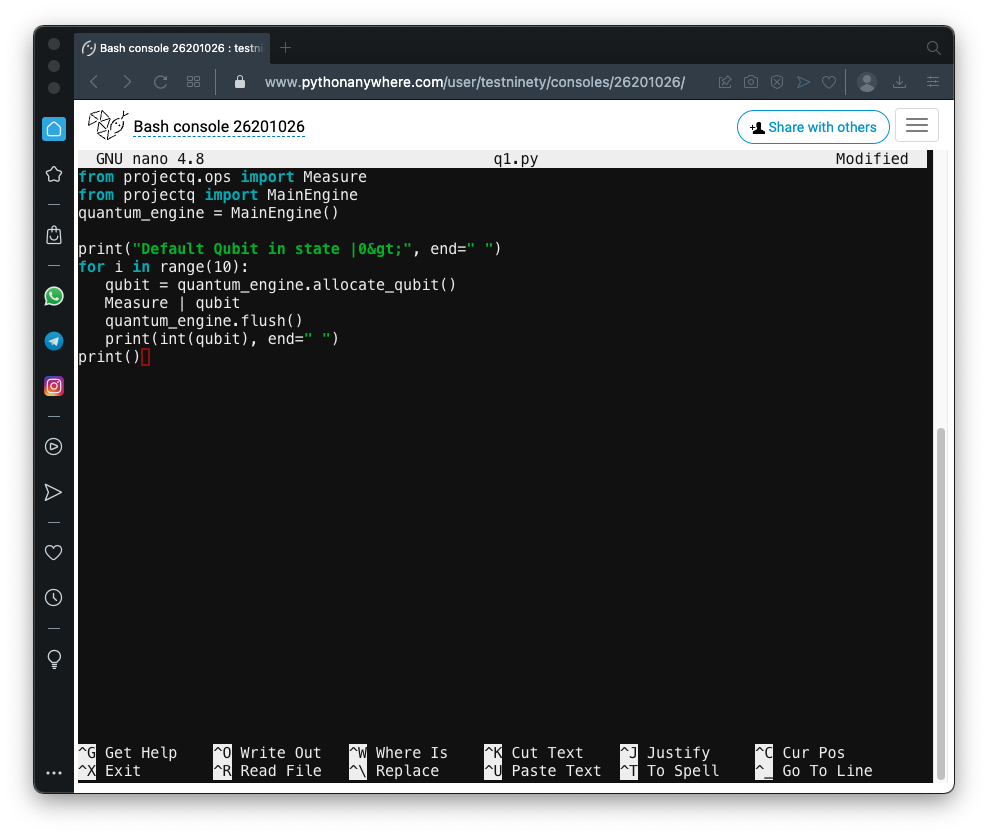
Save the program with Ctrl+X, Y, Enter.

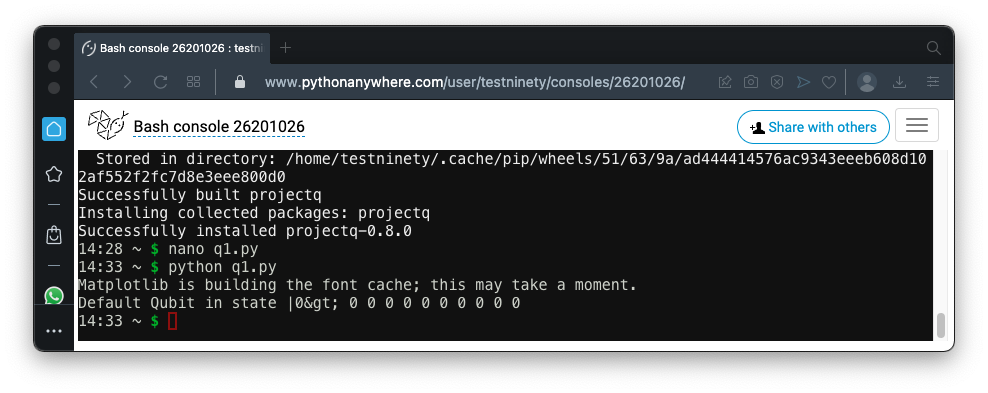
Execute this command to run the program: 

python q1.py
A newly created Qubit is in the state |0>.

Therefore, all ten measurements of the qubit result in 0, as shown below.

Flipping a Qubit with an X Gate

To understand a qubit, look at the Bloch Sphere shown below (from here).

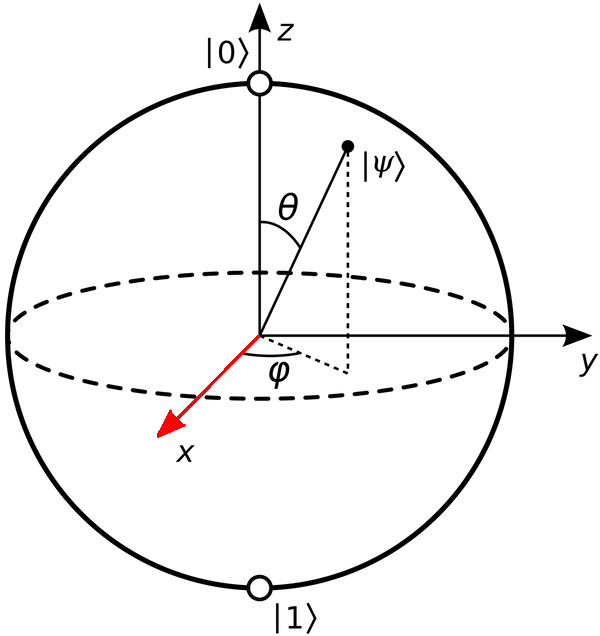
A newly created qubit starts in state |0>, shown as a green arrow in the figure below.

An X-gate rotates the qubit 180 degrees around the X-axis, so the arrow points down, to state |1>.

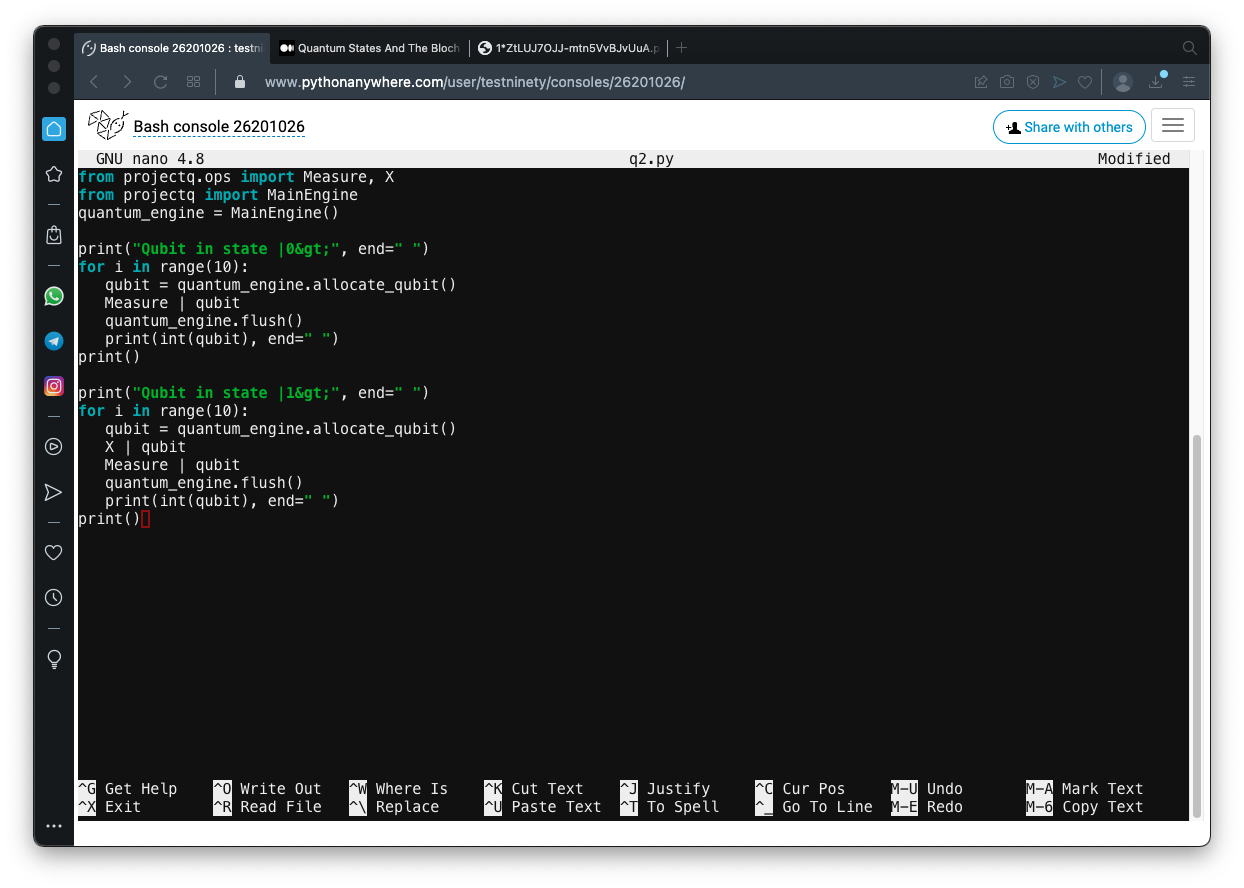
Create a file named q2.py containing this code, as shown below. 

from projectq.ops import Measure, X
from projectq import MainEngine
quantum_engine = MainEngine()

print("Qubit in state |0>", end=" ")
for i in range(10):
   qubit = quantum_engine.allocate_qubit()
   Measure | qubit
   quantum_engine.flush()
   print(int(qubit), end=" ")
print()

print("Qubit in state |1>", end=" ")
for i in range(10):
   qubit = quantum_engine.allocate_qubit()
   X | qubit
   Measure | qubit
   quantum_engine.flush()
   print(int(qubit), end=" ")
print()

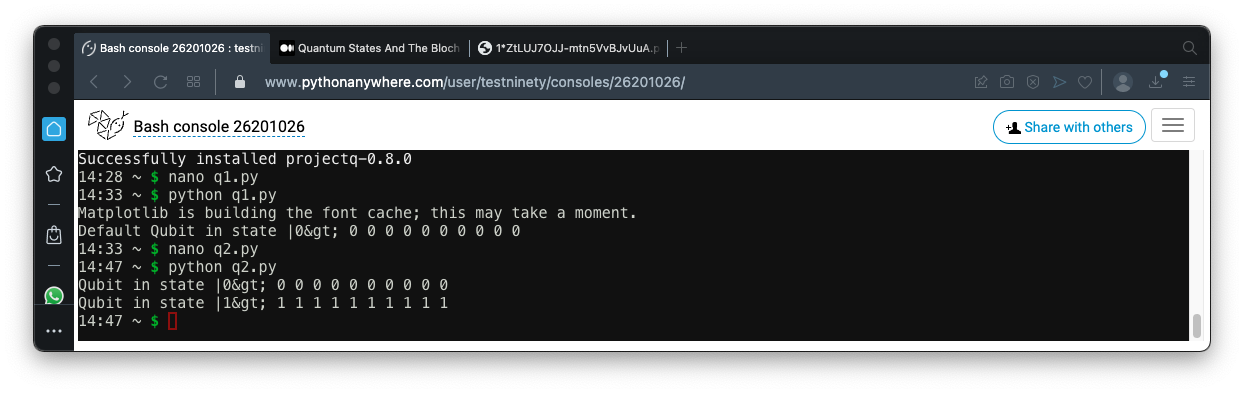
Run the program.

the X gate flips the Qubit to the state |1>. Measuring that Qubit always results in 1, as shown below.

Superposition State

So far we've used Qubits to to the same thing normal bits do. To see the unique properties of Qubits, we need to use "superposition" states that are mixtures of |0> and |1>.

The Hadamard gate moves the Qubit into a superposition state containing equal amounts of |0> and |1>.

This state is represented by the red arrow on the Bloch sphere figure above. (Technically, it should be on the X-axis rather than the Y-axis, but that doesn't matter for what we are doing here.)

In a text editor, create a file named q3.py containing this code: 

from projectq.ops import Measure, H
from projectq import MainEngine
quantum_engine = MainEngine()

print("Qubit in state |0>", end=" ")
for i in range(10):
   qubit = quantum_engine.allocate_qubit()
   Measure | qubit
   quantum_engine.flush()
   print(int(qubit), end=" ")
print()

print("Superposition State: ", end=" ")
for i in range(10):
   qubit = quantum_engine.allocate_qubit()
   H | qubit
   Measure | qubit
   quantum_engine.flush()
   print(int(qubit), end=" ")
print()

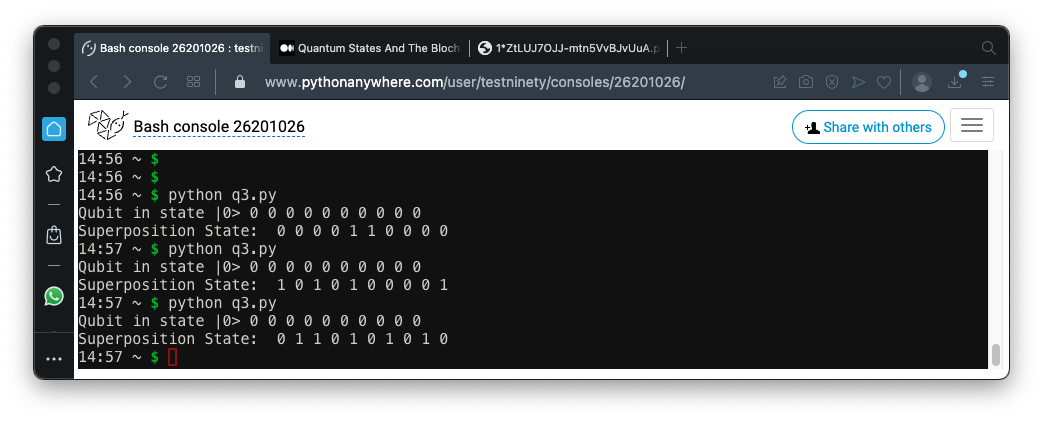
Run the program several times. The superposition state has a 50% chance of being 0 when measured, and a 50% chance of being 1, as shown below.

This is "quantum uncertainty" and it is a fundamental aspect of reality that changed everything about physics. It bothered Einstein, who said "God does not play dice." However, as far as we can tell, Einstein was wrong and this uncertainty is a real property of quantum objects.

Entanglement

It is possible to "entangle" two Qubits, so that they must both have the same value when measured. This is an important feature of Qubits that does not happen with regular bits, and it makes some calculations far faster on quantum computers.

To entangle Qubits, we use the CNOT operator.

In a text editor, create a file named q4.py containing this code: 

from projectq.ops import Measure, H, CNOT
from projectq import MainEngine
eng = MainEngine()

for i in range(10):
   qubit1 = eng.allocate_qubit()
   qubit2 = eng.allocate_qubit()
   H | qubit1
   CNOT | (qubit1, qubit2)
   Measure | qubit1
   Measure | qubit2
   eng.flush()
   print("(", int(qubit1),  int(qubit2), ")", end=" ")
print()

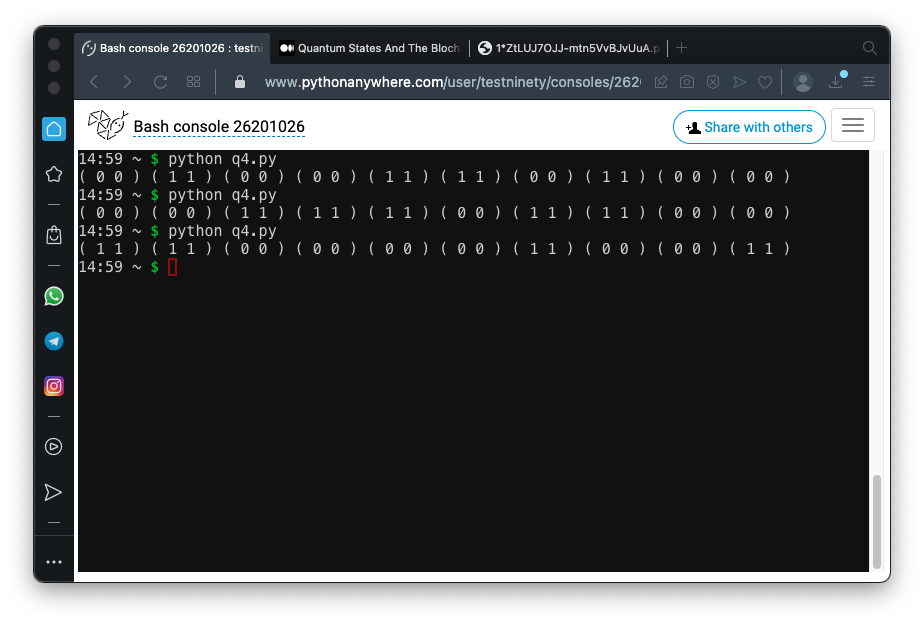
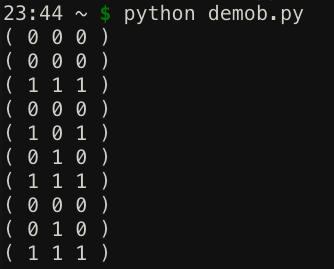
Run the program several times. The Qubits are sometimes 0, sometimes 1, but they are always equal, as shown below.

Pretty Circuit Diagrams

This program creates "tex" files, which are graphic images in a format called LaTeX.

In a text editor, create a file named q5.py containing this code: 

from projectq.ops import Measure, H, CNOT
from projectq import MainEngine
from projectq.backends import CircuitDrawer
drawing_engine = CircuitDrawer()
eng = MainEngine(drawing_engine)

qubit1 = eng.allocate_qubit()
qubit2 = eng.allocate_qubit()
H | qubit1
CNOT | (qubit1, qubit2)
eng.flush()
print(drawing_engine.get_latex())

Execute this command to write a LaTeX file: 

python3 q5.py > q5.tex
At the top right of the PythonAnywhere window, click the three-bar icon.

Click Files.

On the "q5.tex" line, right-click the down-arrow icon, click "Save link as...", and save the file in your Downloads folder.

Use this online conversion site ito convert the tex file to a PDF:

https://www.freefileconvert.com/

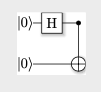
Browse to q5.pdf and double-click it. You see a pretty diagram of your quantum circuit, as shown below.

The two Qubits start in their default states of |0> .

One of them passes through a Hadamard gate, and then they are entangled, denoted by the the ⊕ symbol.

Circuit with Three Qubits

To see a diagram, create this file: 
from projectq.ops import Measure, H, CNOT
from projectq import MainEngine
from projectq.backends import CircuitDrawer
drawing_engine = CircuitDrawer()
eng = MainEngine(drawing_engine)

qubit1 = eng.allocate_qubit()
qubit2 = eng.allocate_qubit()
qubit3 = eng.allocate_qubit()
H | qubit1
CNOT | (qubit1, qubit3)
H | qubit2
eng.flush()
print(drawing_engine.get_latex())
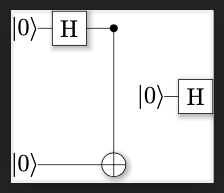
Run the file, and put the output in a .tex file. Convert that file to a PDF.

The circuit is shown below. The first and third qubits are entangled, and the second one stands alone.

To see the qubit values, create this file: 

from projectq.ops import Measure, H, CNOT
from projectq import MainEngine
eng = MainEngine()

for i in range(10):
  qubit1 = eng.allocate_qubit()
  qubit2 = eng.allocate_qubit()
  qubit3 = eng.allocate_qubit()
  H | qubit1
  CNOT | (qubit1, qubit3)
  H | qubit2
  Measure | qubit1
  Measure | qubit2
  Measure | qubit3
  eng.flush()
  print("(", int(qubit1),  int(qubit2), int(qubit3), ")")
print()
As shown below, the first and third qubits are always equal. The second qubit is randomly 0 or 1.

C 510.1: Three Qubits (10 pts)

Program the quantum circuit shown below.

Note that the ⊕ symbol on a single line denotes an X gate.

You will need to import the X function.

Create a second program that measures and prints out the value of the qubits, instead of drawing a diagram.

Run that circuit a few times, printing the three qubits. The answers vary.

Find the answer containing the largest number of ones, and concatenate the bits, like this: 

001
That's the flag.

C 510.2: Five Qubits (10 pts)

Program the quantum circuit shown below.

Note that the ⊕ symbol on a single line denotes an X gate.

Run that circuit a few times, printing the five bits. The answers vary.

Interpret each sequence of five bits into a binary number, and convert it to decimal.

The highest possible value is the flag.

For example, if the bits were 

11111
the flag would be 31.

Sources

IBM Q Beginner's Guide
Quantum Computer Programming Introduction
Tutorial: Getting started with Quantum Computing in Python
Quantum teleportation
ProjectQ Docs Examples

Posted 7-12-2020 by Sam Bowne
PDF instructions updated 12-28-20
Updated to use PythonAnywhere 11-9-22
Flag 1 process explained more, and three-qubit demo added 11-13-23