C 507: Pollard-Rho Attack on DLP (55 pts extra)

What you need:

Purpose

To crack the Discrete Logarithm Problem (DLP) for small key sizes.

DLP Problem Statement

gy = x (mod p)

Pollard-Rho Theory

We'll break the difficult DLP into two easier problems.

Problem 1: Find a Collision

We'll find integers (a, b), and (A, B) such that:
g a x b = g A x B (mod p)
This problem is easier than the DLP because of the birthday paradox.

We'll use an algorithm called the Tortoise and the Hare to solve it.

The Tortoise and the Hare

We'll use this function:
F (u) =

{ gu  if h(u) = 0
u2  if h(u) = 1
xu  if h(u) = 2
Where h(u) is a hash function with an approximately equal chance of having all three values.

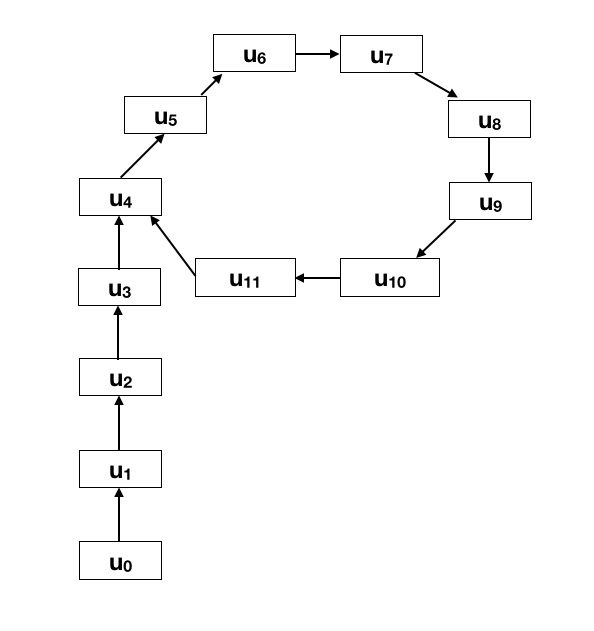
We start with a value u0 and calculate a series of values:

u1 = F (u0)
u2 = F (u1)
u3 = F (u2)   etc.
Eventually, we'll hit a value we've seen before, and after that point, further iterations will just loop through the same series of values, as shown below.

This diagram looks like the greek letter rho, which is why this method is called the Rho method.

The tortoise-and-hare algorithm is a way to find the loop without needing to maintain a table of old values in memory.

We generate two sets of values, the u series (the tortoise) and the v series (the hare), like this:

u1 = F (u0)     v1 = F (F (v0))
u2 = F (u1)     v2 = F (F (v1))
u3 = F (u2)     v3 = F (F (v2))   etc.
The idea is that they both race down the track shown in the figure above, with one moving faster than the other. When they hit the loop, the tortoise will catch up to the hare and the two values will be equal.

When that happens, they will each contain a different number of factors of g and x, so we'll have a collision.

Algorithm for Tortoise and Hare

1. We'll use this hash function: 
import hashlib

def h(u):
   i = (u + 64) % 1256991
   b =  i.to_bytes(3, byteorder="big")
   m = hashlib.md5(b).hexdigest()
   result = int(m, 16) % 3
   return result
2. Define the function F(u) that keeps track of a (the number of g factors) and b (the number of x factors), as shown below. The reason a and b are calculated (mod p - 1) is explained in the Problem 2 section below.
F (u, a, b) =

{ gu  if h(u) = 0; add 1 to a (mod p - 1)
u2  if h(u) = 1; double a and b (mod p - 1)
xu  if h(u) = 2; add 1 to b (mod p - 1)
3. Start out with u and v both equal to 1.

4. Update values:
    Set u to F (u)
    Set v to F (F (v))

5. If u = v, we're done. The result is (a, b) for the Tortoise and (A, B) for the Hare.
    Otherwise go to step 4, unless there have been too many attempts and we give up.

C 507.1: Race (15 pts)

For these values:
  • p = 47
  • g = 7
  • x = 5
Run the race. The flag is the final value of a.

Problem 2: Find y from the Collision

After running the Tortoise and Hare race, we have
g a x b = g A x B (mod p)
In the equation above, replacing x with gy gives:
g a + yb = g A + yB (mod p)
Fermat's little theorem tells us, for any integer c:
c (p - 1) = 1 (mod p)
Therefore we can remove factors of (p - 1) from the exponents:
g (a + bv) (mod (p - 1)) = g (A + Bv) (mod (p - 1)) (mod p)
a + bv = A + yB (mod p - 1)
Rearranging terms:
(b - B) y = (A - a) (mod p - 1)
Let G be the greatest common denominator of (b - B), (A - a), and (p - 1).

Then each of those terms can be written as G times another integer, indicated by prime marks, like this:

(b' - B' ) Gy = G (A' - a' ) (mod G p' )
Since every term is an integral multiple of G, we can just rescale this statement (see gray box below), measuring every term in units of G and make the ring smaller by a factor of G, like this:
(a' - A' ) y = (B' - b' ) (mod p' )
So:
y = (A' - a' ) (b' - B' ) -1 (mod p' )
This formula gives us y (mod p' ), which we'll call y0, so any of these values might be the real y:
y = y0 + kp'
We don't know k so we'll have to try many values to find a solution.

Scaling

Consider this equation:
900 = 100 (mod 800)
If all the quantities in this equation are divisible by 100, we can renumber the ring in units of 100 without losing any information, since the numbers 1-99, 101-199, etc. are never used:
9 = 1 (mod 8)
This is a situation common in physics, like switching the units of measurement from meters to inches.

Algorithm for Problem 2: Find y from the Collision

1. GCD: Find G, the greatest common denominator of these three numbers:
  • (b - B) (mod p - 1)
  • (A - a) (mod p - 1)
  • p - 1
2. Calculate (b' - B' ), (A' - a'), and p' by dividing those three numbers by G.

3. Calculate the modular inverse (b' - B' ) -1 (mod p' )
    Calculate y0 = (A' - a' ) (b' - B' ) -1 (mod p' )

4. Loop through values of k = 0, 1, 2, 3, ...
    Calculate y = y0 + kp' . If gy = x, we're done.

C 507.2: GCD (10 pts)

Find the GCD of these numbers:
  • 39199007823998693533
  • 32254013411746110071
  • 56652933174483971459
The flag is the GCD value.

Hint: use PyCryptodome

C 507.3: Inverse (5 pts)

Find a -1 (mod p' ) for these values:
  • a = 5
  • p' = 4093082899
The flag is the value of a -1.

C 507.4: DLP (15 pts)

Given:
gy = x (mod p)
Find y from these values:
  • p = 777777
  • g = 1971
  • x = 22173
The flag is the value of y.

C 507.5: DLP (10 pts)

Given:
gy = x (mod p)
Find y from these values:
  • p = 22333555577777
  • g = 197119721973
  • x = 17728870310451
The flag is the value of y.

References

Cycle detection From Wikipedia
A Quick Tutorial on Pollard's Rho Algorithm
Pollard rho Factorization Method
The Pollard-Rho attack on Diffie Hellman
NCC Group Whitepaper: How to Backdoor Diffie-Hellman
Pollard's rho algorithm for logarithms
Linear Feedback Shift Registers for the Uninitiated, Part V: Difficult Discrete Logarithms and Pollard's Kangaroo Method

Posted 9-10-20 by Sam Bowne
11-11-21: Point total corrected