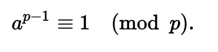
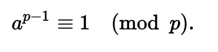
So testing that condition for several random values of a can be used as evidence that p is probably prime.
This site explains the Fermat primality test and its flaws in more detail:
https://en.wikipedia.org/wiki/Fermat_primality_test
from random import randint
p = int(input("Input potential prime: "))
for i in range(5):
a = randint(2,p-2)
if pow(a, p-1, p) == 1:
print("PASS for ", a)
else:
print("FAIL for ", a)
print()
python3 fermat.py
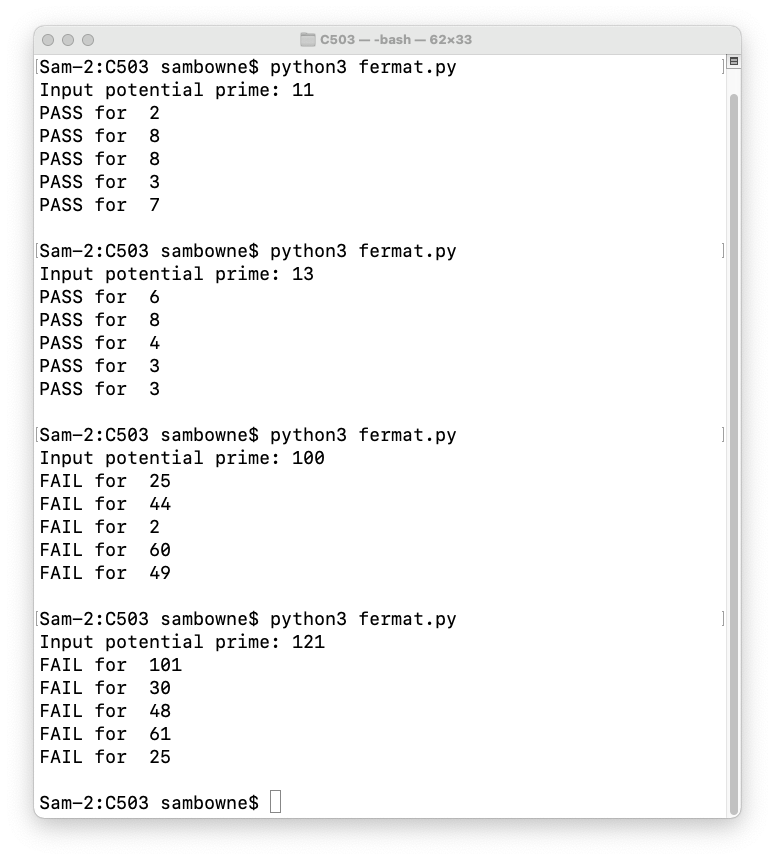
As shown below, 11 and 13 pass all the tests because they are prime, but 100 and 121 fail because they aren't.
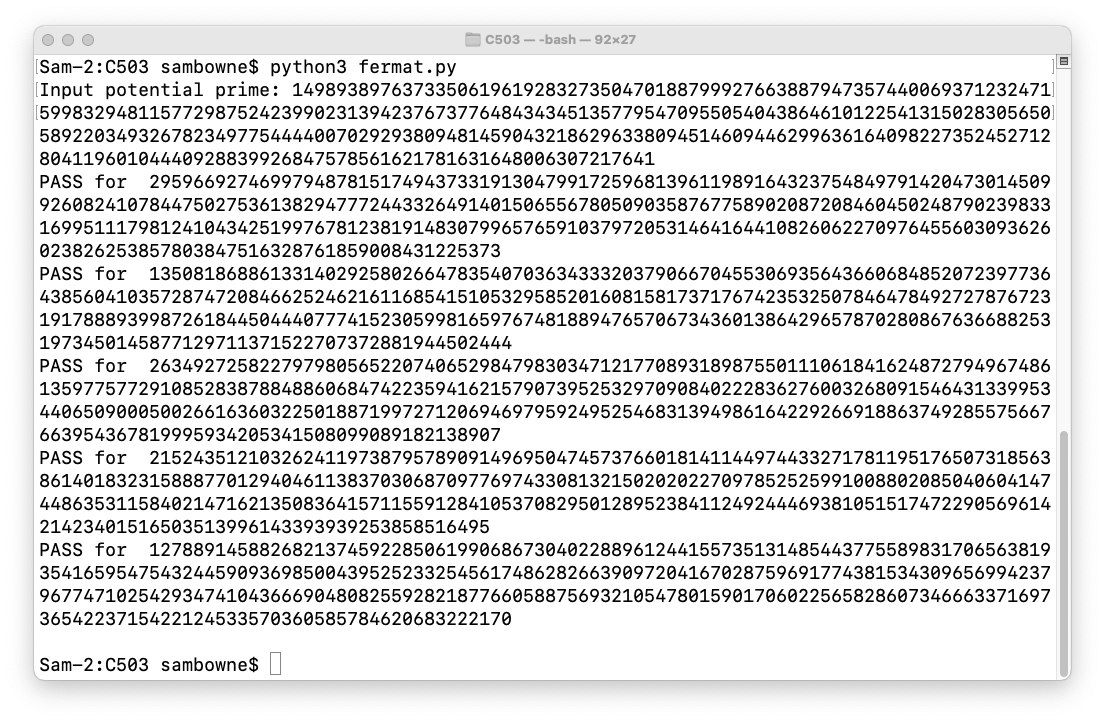
149893897637335061961928327350470188799927663887947357440069371232471599832948115772987524239902313942376737764843434513577954709550540438646101225413150283056505892203493267823497754444007029293809481459043218629633809451460944629963616409822735245271280411960104440928839926847578561621781631648006307217641
It works, because Python really can handle any size of integer, as shown below.
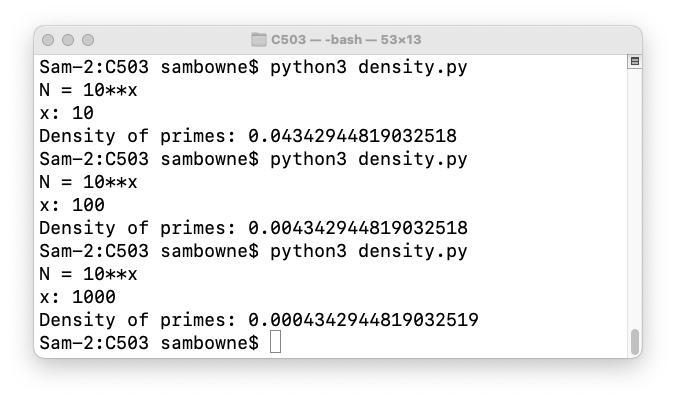
1 / ln(N)Or, in Python:
import math
print("N = 10**x")
x = int(input("x: "))
n = 10**x
print("Density of primes:", 1/math.log(n))
C 503.1: Find the Next Prime (10 pts)
This number is not prime:10**300
Find the first number above it which is prime.
The flag is that number as one long integer, like
11111111111111111111111111111111
C 503.2: Companion Primes (10 pts extra)
11 and 13 are both primes, only differing by two. Such primes are called companion primes.Find the first set of companion primes above
10**100
The flag is the lower of the two primes, as one long integer, like
11111111111111111111111111111111