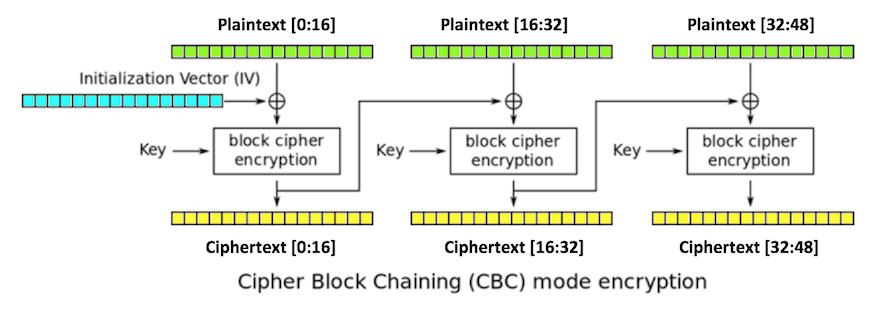
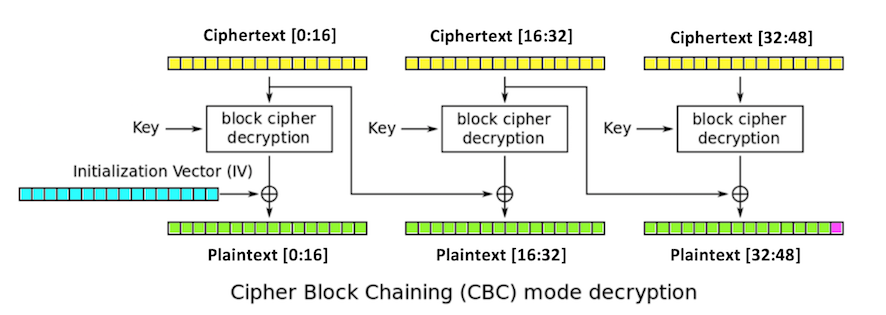
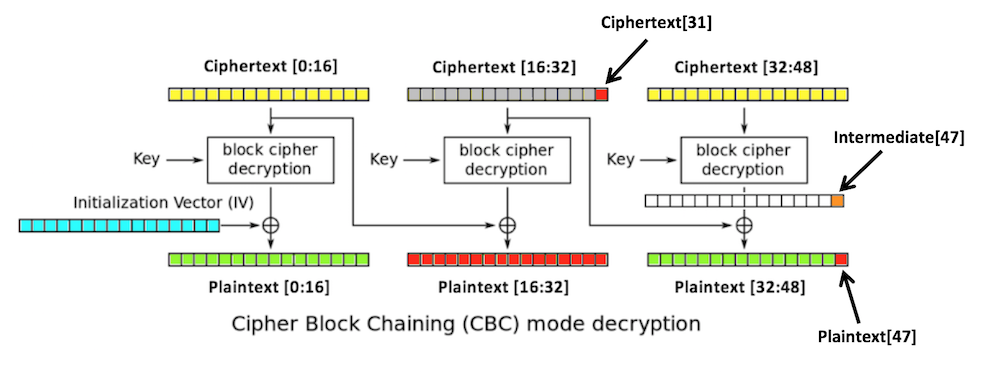
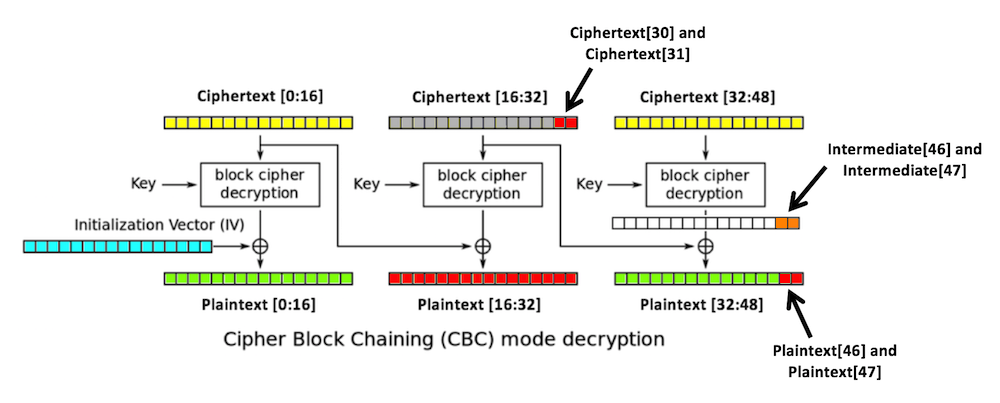
Three blocks of plaintext (green), each 16 bytes long, are encrypted, producing three blocks of ciphertext (yellow).
The first block is XORed with an initialization vector or iv (blue), also 16 bytes long, and then encrypted with the key.
Each subsequent block is XORed with the previous block of ciphertext.

01
0202
030303
0f0f0f0f0f0f0f0f0f0f0f0f0f0f0f
10101010101010101010101010101010
plaintext[47] == chr(1)
ciphertext[31]
plaintext[16:32]
plaintext[47]
python
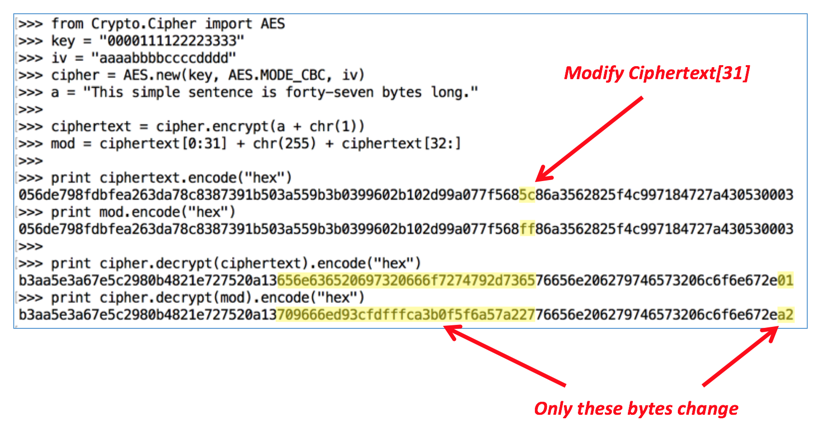
from Crypto.Cipher import AES
key = "0000111122223333"
iv = "aaaabbbbccccdddd"
cipher = AES.new(key, AES.MODE_CBC, iv)
a = "This simple sentence is forty-seven bytes long."
ciphertext = cipher.encrypt(a + chr(1))
mod = ciphertext[0:31] + chr(255) + ciphertext[32:]
print ciphertext.encode("hex")
print mod.encode("hex")
print cipher.decrypt(ciphertext).encode("hex")
print cipher.decrypt(mod).encode("hex")
Use a text editor, such as nano or Notepad, to make this file. Save it as pador.py in your home directory.
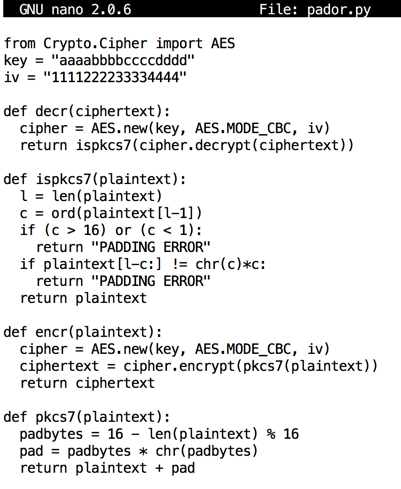
from Crypto.Cipher import AES
key = "aaaabbbbccccdddd"
iv = "1111222233334444"
def decr(ciphertext):
cipher = AES.new(key, AES.MODE_CBC, iv)
return ispkcs7(cipher.decrypt(ciphertext))
def ispkcs7(plaintext):
l = len(plaintext)
c = ord(plaintext[l-1])
if (c > 16) or (c < 1):
return "PADDING ERROR"
if plaintext[l-c:] != chr(c)*c:
return "PADDING ERROR"
return plaintext
def encr(plaintext):
cipher = AES.new(key, AES.MODE_CBC, iv)
ciphertext = cipher.encrypt(pkcs7(plaintext))
return ciphertext
def pkcs7(plaintext):
padbytes = 16 - len(plaintext) % 16
pad = padbytes * chr(padbytes)
return plaintext + pad
python
from pador import encr, decr
a = "This simple sentence is forty-seven bytes long."
c = encr(a)
print c.encode("hex")

d = decr(c)
print d
print d.encode("hex")

mod = c[0:47] + chr(65)
decr(mod)
decr(c)
This seemingly harmless error message is enough to completely defeat the encryption, because it can be used to leak out information about the encryption process.

WIN
You have a single example of encrypted text, and a system that will let you test encrypted text and tell you whether the padding is correct or not.
This should be impossible, but it can be done using the padding oracle attack.
intermediate[32:48],
depends only on the key and the third
block of ciphertext.
If we can figure out the intermediate state, we can create ciphertext that decrypts to any plaintext we want in the third block. We do that by modifying the second block.
We don't need to know the key or the iv.
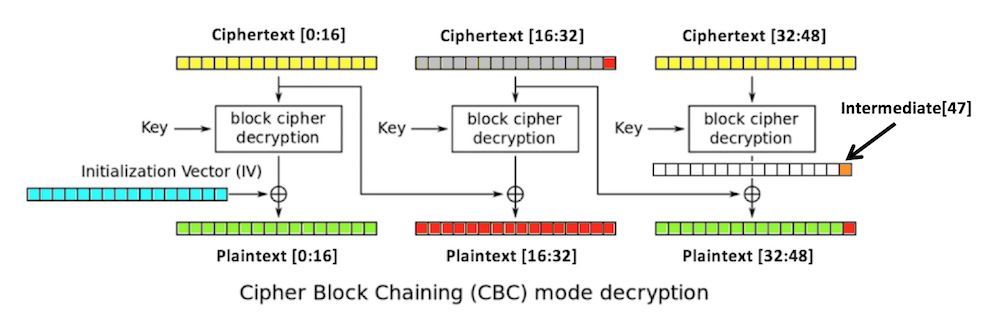
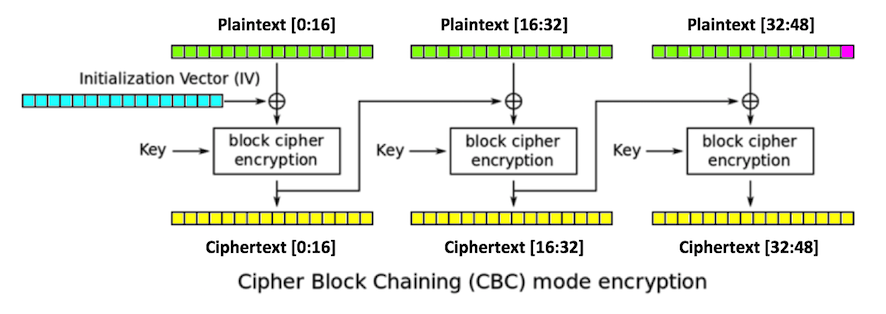
1. You start with a valid ciphertext string.
2. Replace ciphertext[16:32] with any random
bytes. This will change the second and third
blocks of plaintext, including the last byte
of plaintext,
plaintext[47],
which is colored red in
the figure below.
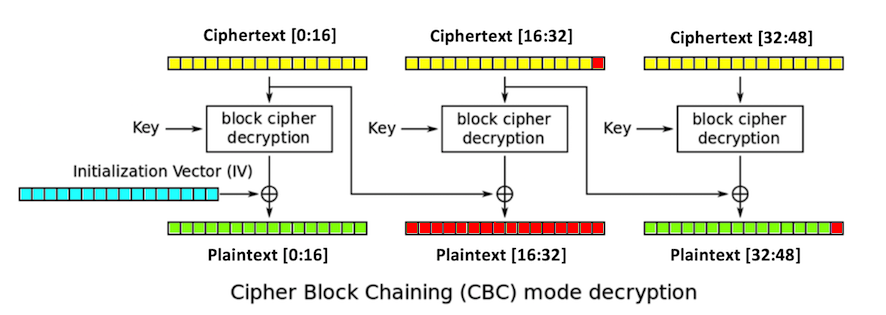
The padding of the plaintext will now be
invalid, unless plaintext[47]
is 1. (There's a small chance that it might be valid
in other ways, but let's ignore that for now.)
3. Try all possible byte values for
ciphertext[31]
until a valid padding is found. Now we know that
plaintext[47] is 1.
4. The last intermediate byte is the XOR of those values:
ciphertext[31] ^ 1
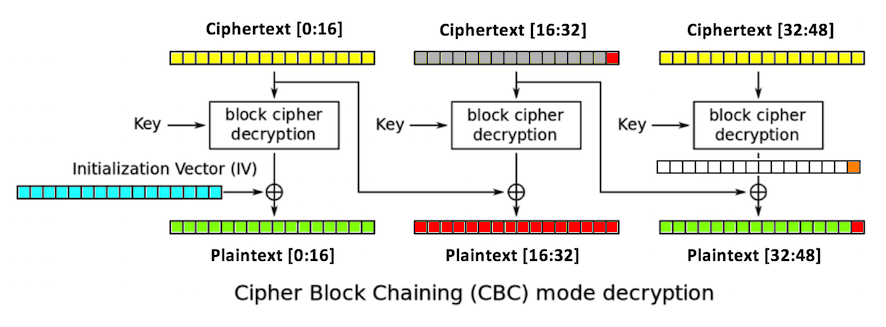
After 256 guesses, we get one byte of the intermediate value. We can continue in this fashion until we get them all, except for the first block.
a = "This sentence cleaarly says I'M A LOSER."
original = encr(a)
print original.encode("hex")

Now we are ready to perform the attack in four stages, as detailed below.
for i in range(5):
mod = original[0:31] + chr(i) + original[32:]
print i, decr(mod)

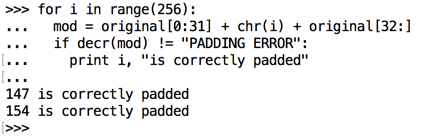
for i in range(256):
mod = original[0:31] + chr(i) + original[32:]
if decr(mod) != "PADDING ERROR":
print i, "is correctly padded"
One of these is the original byte, which results in a correct string of padding bytes, and the other one results in a final byte of 1, which is interpreted as a correct padding string one byte long.
Execute this command to see the original value of ciphertext[31].
print ord(original[31])

This was effective, but it would be better to find the value directly, instead of finding two possibilities and needing to choose between them.
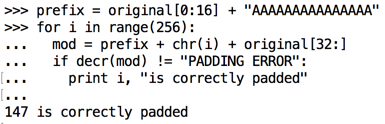
prefix = original[0:16] + "AAAAAAAAAAAAAAA"
for i in range(256):
mod = prefix + chr(i) + original[32:]
if decr(mod) != "PADDING ERROR":
print i, "is correctly padded"
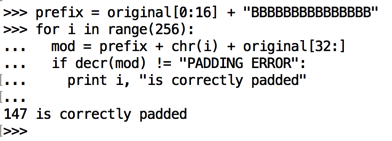
prefix = original[0:16] + "BBBBBBBBBBBBBBB"
for i in range(256):
mod = prefix + chr(i) + original[32:]
if decr(mod) != "PADDING ERROR":
print i, "is correctly padded"
ciphertext[31] ^ intermediate[47] = plaintext[47]
Applying ciphertext[31] ^ to both sides of this equation yields:
ciphertext[31] ^ ciphertext[31] ^ intermediate[47] = ciphertext[31] ^ plaintext[47]Rearranging terms yields:
intermediate[47] ^ ciphertext[31] ^ ciphertext[31] = ciphertext[31] ^ plaintext[47]On the left side, intermediate[47] is XORed with a byte, and then XORed again with the same byte. XOR is its own inverse--XORing twice with the same byte gets you back where you started, so:
intermediate[47] = ciphertext[31] ^ plaintext[47]And we know that plaintext[47] must be 1 to make the padding valid, so, when the padding is valid,
intermediate[47] = ciphertext[31] ^ 1 = 147 ^ 1 = 146So now we know this:
intermediate[47] = 146
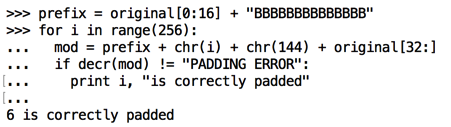
intermediate[47] = 146So we need to use this value of ciphertext[31]:plaintext[47] = 2
ciphertext[31] = 146 ^ 2 = 144
prefix = original[0:16] + "BBBBBBBBBBBBBB"
for i in range(256):
mod = prefix + chr(i) + chr(144) + original[32:]
if decr(mod) != "PADDING ERROR":
print i, "is correctly padded"
We can now calculate Intermediate[46]
intermediate[46] = ciphertext[30] ^ plaintext[46] = 6 ^ 2 = 4So now we know this:
intermediate[46] = 4
intermediate[47] = 146
intermediate[46] = 4So we need to use these values for ciphertext[30] and ciphertext[31]:
intermediate[47] = 146plaintext[46] = 3
plaintext[47] = 3
ciphertext[30] = 4 ^ 3 = 7
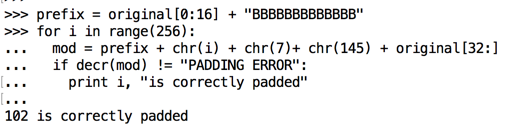
ciphertext[31] = 146 ^ 3 = 145
Press Enter twice after the last line of text.
prefix = original[0:16] + "BBBBBBBBBBBBB"
for i in range(256):
mod = prefix + chr(i) + chr(7) + chr(145) + original[32:]
if decr(mod) != "PADDING ERROR":
print i, "is correctly padded"
We can now calculate Intermediate[45]
intermediate[45] = ciphertext[29] ^ plaintext[45] = 102 ^ 3 = 101So now we know this:
intermediate[45] = 101
intermediate[46] = 4
intermediate[47] = 146
intermediate[45] = 101So we need to use these values for ciphertext[29], ciphertext[30], and ciphertext[31]:
intermediate[46] = 4
intermediate[47] = 146plaintext[45] = 4
plaintext[46] = 4
plaintext[47] = 4
ciphertext[29] = 101 ^ 4 = 97
ciphertext[30] = 4 ^ 4 = 0
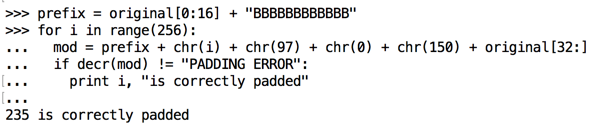
ciphertext[31] = 146 ^ 4 = 150
Press Enter twice after the last line of text.
prefix = original[0:16] + "BBBBBBBBBBBB"
for i in range(256):
mod = prefix + chr(i) + chr(97) + chr(0) + chr(150) + original[32:]
if decr(mod) != "PADDING ERROR":
print i, "is correctly padded"
We can now calculate Intermediate[44]
intermediate[44] = ciphertext[28] ^ plaintext[44] = 235 ^ 4 = 239So now we know this:
intermediate[44] = 239
intermediate[45] = 101
intermediate[46] = 4
intermediate[47] = 146
intermediate[44] = 239We want this plaintext, ending with "WIN" and a correct single byte of 1 for padding:
intermediate[45] = 101
intermediate[46] = 4
intermediate[47] = 146
cleartext[44] = ord("W")So we choose these ciphertext bytes:
cleartext[45] = ord("I")
cleartext[46] = ord("N")
cleartext[47] = 1
ciphertext[28] = cleartext[44] ^ intermediate[44] = ord("W") ^ 239Execute these commands to calculate and insert those bytes (it's a little clumsy because Python doesn't let you assign a byte inside a string):
ciphertext[29] = cleartext[45] ^ intermediate[45] = ord("I") ^ 101
ciphertext[30] = cleartext[46] ^ intermediate[46] = ord("N") ^ 4
ciphertext[31] = cleartext[47] ^ intermediate[47] = 1 ^ 146
c28 = ord("W") ^ 239
c29 = ord("I") ^ 101
c30 = ord("N") ^ 4
c31 = 1 ^ 146
ciphertext = original[0:28] + chr(c28) + chr(c29) + chr(c30) + chr(c31) + original[32:]
decr(ciphertext)

Open a Terminal window and execute these commands:
cd Downloads
mv padorchal1.pyx padorchal1.py
python
from padorchal1 import decr
a = "3ceafc6720f418f86b937a14fa0703df352b04f7d1e6a1e3bdd2e6f36e3da543800a6b07b3db36b372e934dfeeb2d920"
decr(a)
c="aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
decr(c)

This ciphertext is valid:
3ceafc6720f418f86b937a14fa0703df352b04f7d1e6a1e3bdd2e6f36e3da543800a6b07b3db36b372e934dfeeb2d920
Put this name on the winners board: EXAMPLE
To get on the winners board, send ciphertext in hex
that decodes to a string ending in :YOURNAME
with correct padding.
Use the form below to put your name on the WINNERS PAGE.
When you get it, tell your instructor to collect your points. This challenge does not have a flag to enter into the automated scoring system.