
How large are p and q? Well, they can't both be larger than the square root of n, or they'd be larger than n when multiplied together.
Start Python in interactive mode. On a Mac or Linux box, you can do that by typing this command into a Terminal window:
python
import math
n = 10142789312725007
print math.sqrt(n)
Execute this command:
print repr(math.sqrt(n))
A good way to do this is to calculate n mod c, where c is a candidate. If c is a factor of n, the result will be zero.
We can test the first 20 candidates with a for loop.
Execute these commands:
c = 100711413
for i in range(c, c-40, -2):
print i, n%i
The third candidate is the winner, with a remainder of zero, as shown below.
Execute these commands:
p = 100711409
q = n / p
print p, q, n, p*q, n - p*q
phin = (p-1) * (q-1)
print p, q, n, phin
Open a new Terminal window, not the one running Python, and execute this command to download and install a few dependencies and gmpy:
brew install gmp mpfr mpc
pip install gmpy
brew install python
apt install python-gmpy
In a Web browser, go to:
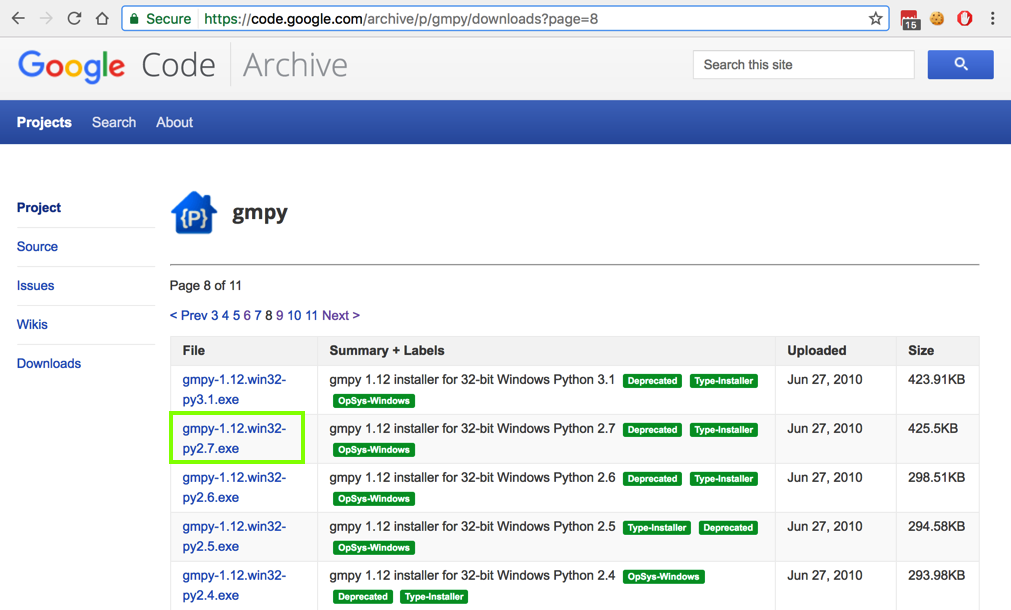
https://code.google.com/archive/p/gmpy/downloads?page=8
Download gmpy-1.12.win32-py2.7.exe, as shown below. Double-click this file and install it with the default options.
If you are using a later version of Windows, you might need a more recent version of gmpy from this page . These downloads are "wheel" files, and must be installed from a command prompt with the "pip install" command.
(d * e) mod phin = 1d is the "multiplicative inverse" of e.
We know that e = 5 from the Problem Statement.
It's not obvious how to find d, but there's a simple way to do it in Python, using the "gmpy" library.
In the Terminal window running python, execute these commands.
e = 5
import gmpy
d = gmpy.invert(e, phin)
print d, e, d*e %phin
Hi!
In the Terminal window running python, execute these commands.
x1 = ord('H')
x2 = ord('i')
x3 = ord('!')
x = x1*256*256 + x2*256 + x3
print x
Execute these commands:
y = x ** e % n
print y
Execute this command:
xx = y ** d % n
To compute such a number, we must use the pow() function.
Execute these commands to restart python and restore all the values we calculated previously:
python
n = 10142789312725007
p = 100711409
q = 100711423
phin = (p-1) * (q-1)
e = 5
import gmpy
d = gmpy.invert(e, phin)
x1 = ord('H')
x2 = ord('i')
x3 = ord('!')
x = x1*256*256 + x2*256 + x3
y = x ** e % n
Let's try that decryption again with the pow() function. Execute these commands:
xx = pow(y, d, n)
print xx
xx1 = xx / (256*256)
xx2 = (xx - 256*256*xx1) / 256
xx3 = xx - 256*256*xx1 - 256*xx2
msg = chr(xx1) + chr(xx2) + chr(xx3)
print xx1, xx2, xx3, msg
Hint 1: The message, converted to a decimal number, is 7 digits long and ends in 43.WOW
Hint 2: The encrypted message is 16 digits long and ends in 66.
The flag is the encrypted message.
Hint 1: The message, converted to a decimal number, is 12 digits long and ends in 41.OBEY!
Hint 2: The encrypted message is 16 digits long and ends in 81.
The flag is the encrypted message.
Meghan sends this message to Cueball. Decrypt it.(111036975342601848755221, 13)
The flag is the decrypted message.80564890594461648564443
Meghan sends this message to Rob. Decrypt it.(1234592592962967901296297037045679133590224789902207663928489902170626521926687, 5557)
Hint: Make square root calculations more precise.272495530567010327943798078794037733865151017104532777645776936985235709526002
The flag is the decrypted message.
Prime Numbers Generator and Checker
Arbitrary precision of square roots