CBL 7: RSA Encryption (170 pts)

RSA Key Generation

Let's start with these prime numbers: 
p = 7
q = 23
Key generation works as shown in the figure below, from this book.

In addition to p and q, we need to choose e. Let's use: 

e = 5

Enter this program into a file named rsa.cbl: 

IDENTIFICATION DIVISION.  
   PROGRAM-ID. RSA.  
  
DATA DIVISION.  
   WORKING-STORAGE SECTION.  
      01 WS-X PIC 9(36).
      01 WS-N PIC 9(36).
      01 WS-D PIC 9(36).

      01 WS-P PIC 9(36).
      01 WS-Q PIC 9(36).
      01 WS-P1 PIC 9(36).
      01 WS-Q1 PIC 9(36).
      01 WS-E PIC 9(36).
      01 WS-PHI PIC 9(36).
      01 WS-DIV PIC 9(36).
      01 WS-REM PIC 9(36).

PROCEDURE DIVISION.  
   DISPLAY "ENTER P:".
   ACCEPT WS-P.
   DISPLAY "ENTER Q:".
   ACCEPT WS-Q.
   DISPLAY "ENTER E:".
   ACCEPT WS-E.

   MULTIPLY WS-P BY WS-Q GIVING WS-N.
   DISPLAY "N = " WS-N

   SUBTRACT 1 FROM WS-P GIVING WS-P1. 
   SUBTRACT 1 FROM WS-Q GIVING WS-Q1. 
   MULTIPLY WS-P1 BY WS-Q1 GIVING WS-PHI.
   DISPLAY "PHI = " WS-PHI.

   DIVIDE WS-PHI BY WS-E GIVING WS-DIV REMAINDER WS-REM.
   IF WS-REM = 0 THEN
      DISPLAY "ERROR: E MUST NOT BE A DIVISOR OF PHI"
      STOP RUN.

   CALL 'MODINV36' USING WS-E, WS-PHI, WS-D.
   DISPLAY 'D = ' WS-D.

STOP RUN.
Create the "MODINV36" subroutine based on the modular inverse routine you created in the previous set of challenges.

Compile it with that file, so you can calculate RSA keys, as shown below.

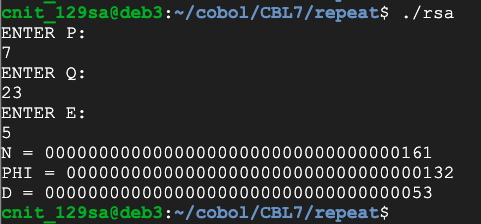
Flag CBL 7.1: Generate D (10 pts)

Calculate d from these values: 
p = 17
q = 43
e = 5

Encoding a Message

Consider this message: 
AB
Let's encode each character using ASCII values in base 10, forming two numbers like this: 
65 66

RSA Encryption

To encrypt a number x with a public key (n, e), use this formula:

So this program will encrypt a single character with e=5: 

IDENTIFICATION DIVISION.  
   PROGRAM-ID. RSA-EN5.  
  
DATA DIVISION.  
   WORKING-STORAGE SECTION.  
      01 WS-X PIC 9(36).
      01 WS-N PIC 9(36).
      01 WS-Y PIC 9(36).
      01 WS-DIV PIC 9(36).

PROCEDURE DIVISION.  
   DISPLAY 'ENTER X:'.
   ACCEPT WS-X.
   DISPLAY 'ENTER N:'.
   ACCEPT WS-N.
   DISPLAY 'USING E = 5'.

   MULTIPLY WS-X BY WS-X GIVING WS-Y.
   MULTIPLY WS-X BY WS-Y GIVING WS-Y.
   MULTIPLY WS-X BY WS-Y GIVING WS-Y.
   MULTIPLY WS-X BY WS-Y GIVING WS-Y.

   DIVIDE WS-Y BY WS-N GIVING WS-DIV REMAINDER WS-Y.
   DISPLAY "Y = " WS-Y.
STOP RUN.
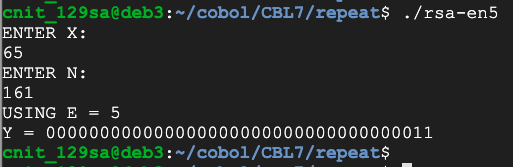
As shown below, that character encrypts to 11.

Flag CBL 7.2: Encrypt (10 pts)

Write a progam that encrypts a series of letters, as shown below.

Encrypt the message FLAG in the same manner with this public key: 

n = 731
e = 5
The result is a 12-digit number. That 12-digit number is the flag.

RSA Decryption

To decrypt a number y with a private key d and a modulus of n, use this formula:

So this program will decrypt a single character: 

IDENTIFICATION DIVISION.
   PROGRAM-ID. RSA-DE.

DATA DIVISION.
   WORKING-STORAGE SECTION.
      01 WS-X PIC 9(36).
      01 WS-N PIC 9(36).
      01 WS-Y PIC 9(36).
      01 WS-D PIC 9(36).
      01 WS-I PIC 9(36).
      01 WS-DIV PIC 9(36).

PROCEDURE DIVISION.
   DISPLAY "ENTER Y:".
   ACCEPT WS-Y.
   DISPLAY "ENTER D:".
   ACCEPT WS-D.
   DISPLAY "ENTER N:".
   ACCEPT WS-N.

   MOVE 1 TO WS-X.
   PERFORM VARYING WS-I FROM 1 BY 1 UNTIL WS-I > WS-D
      MULTIPLY WS-Y BY WS-X GIVING WS-X
      DIVIDE WS-X BY WS-N GIVING WS-DIV REMAINDER WS-X
   END-PERFORM.
   DISPLAY "X = " WS-X.
STOP RUN.
Here's that program decrypting the ciphertext 11 we encrypted earlier with these parameters: 
p = 7
q = 23
e = 5
n = 161
d = 53
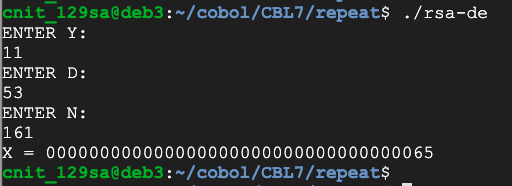
As shown below, that character decrypts to 65.

Flag CBL 7.3: Decrypt (10 pts)

Write a progam that decrypts a series of letters, as shown below.

Challenge: use these parameters: 

p = 7
q = 23
e = 5
n = 161
d = 53
and decrypt this message: 
037088026011033029008078011
The result is the flag.

Flag CBL 7.4: Decrypt without the Key (20 pts)

Using this public key: 
n = 670661
e = 5
Factor that key and find p, q, and d. Then decode this message. Each number is one encrypted letter. 
208489
058442
151261
151261
049897
655085
248257
049897
135963
The result is the flag.

Testing Speed for Multiplicative Inverses

Use your RSA program to calculate D from these values: 
p = 881
q = 883
e = 13
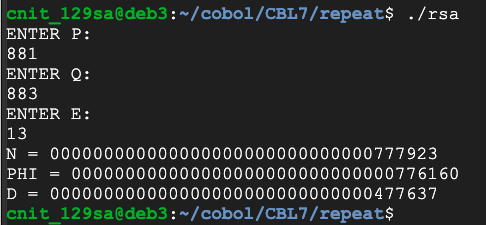
Notice that D is over 400,000 and N is over 700,000, as shown below.

Now use these values: 

p = 7349
q = 7351
e = 13
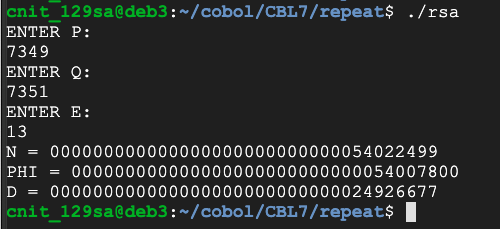
D and N are now in the tens of millions, as shown below, and the calculation is slow, taking about 30 seconds when I did it.

Clearly we can't handle keys much larger than this with the inefficient algorithm we've been using.

Flag CBL 7.5: Euclid's Algorithm (20 pts)

To handle larger keys, we need a faster way to find multiplicative inverses.

Write a faster function to calculate d using Euclid's Algorithm. Change all variables to PIC 9(36), the maximum available in COBOL.

Calculate d from these values: 

p: 7777867
q: 8888933
e: 5
The result is the flag, covered by a green rectangle in the image below.

Testing Speed for Exponentiation

Use your RSA-DE program to calculate X from these values: 
y = 198174
d = 477637
n = 777923
The result is 65, as shown below.

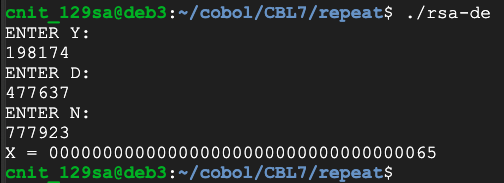
Now use these values: 

y = 32179356
d = 24926677
n = 54022499
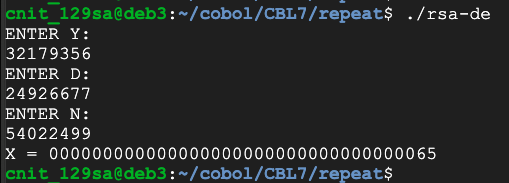
D and N are now in the hundreds of millions, as shown below, and the calculation is slow, taking about 30 seconds when I did it.

Clearly we can't handle keys much larger than this with the inefficient algorithm we've been using.

Flag CBL 7.6: Modular Exponentiation (20 pts)

To handle larger keys, we need a faster way to raise numbers to high powers.

Write a faster function using modular exponentiation.

Calculate x from this function:

with these values: 

y: 5277319168
d: 27654768791645
n: 69136938645911
The result is the flag, covered by a green rectangle in the image below.

Flag CBL 7.7: Finding Large Primes (20 pts)

Fermat's little theorem states that if p is prime and a is not divisible by p, then:

So testing that condition for several random values of a can be used as evidence that p is probably prime. This page explains the Fermat primality test and its flaws in more detail.

Find the first prime number larger than this value: 

999888777666555
The result is the flag, covered by a green rectangle in the image below.

Flag CBL 7.8: Factoring a Number (20 pts)

There are faster algorithms, but simply attempting division by every odd number up to the square root of a number is sufficient to find the factors of a number.

Find the lower factor of this value: 

21188802353371
The result is the flag.

Flag CBL 7.9: Decrypt without the Key (40 pts)

Using this public key: 
n = 68325320563030249
e = 3
Factor that key and find p, q, and d. Then decode this message. 
52281470188782133
The result is a long number. Each pair of digits in that number is the ASCII code for one letter, like this:

The number 656667 encodes the message ABC

The message is the flag.

Posted 4-13-2020 by Sam Bowne