CBL 6: ASCII and Modular Arithmetic (60 pts)

Encoding Text

Enter this program into a file named convert.cbl: 
IDENTIFICATION DIVISION.  
   PROGRAM-ID. CONVERT.  
  
DATA DIVISION.  
   WORKING-STORAGE SECTION.  
      01 WS-LETTER PIC A(1).
      01 WS-CODE PIC 9(2).
  
PROCEDURE DIVISION.  
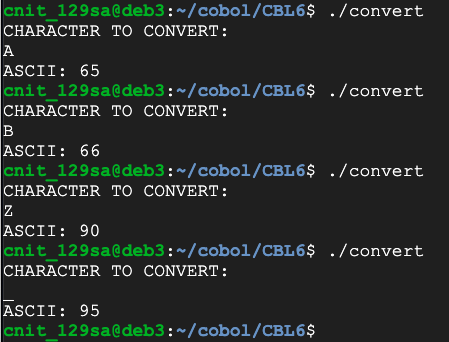
   DISPLAY 'CHARACTER TO CONVERT:'.
   ACCEPT WS-LETTER.
   CALL 'TOASCII' USING WS-LETTER, WS-CODE.
   DISPLAY 'ASCII: ' WS-CODE.
STOP RUN.
Create the "toascii" subroutine and compile it with that file, so you can convert characters to ASCII codes, as shown below.

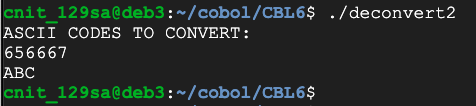
Then create the inverse program, converting ASCII codes back to characters, as shown below.

Flag CBL 6.1: ASCII (10 pts)

Convert these codes to ASCII to see the flag. There are two digits per character. 
847269957076657195738395658367737367796869

Modular Arithmetic

Consider the "Modulus 9" ring shown below. The only numbers used are 0 through 8. Adding 1 to 8 gets you back to zero.

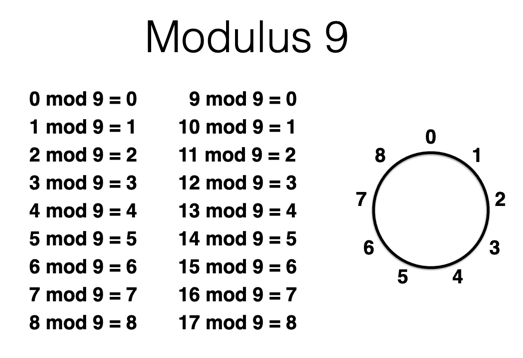
Mathematically, you can compute a number N mod 9 by computing N/9 and keeping the remainder.

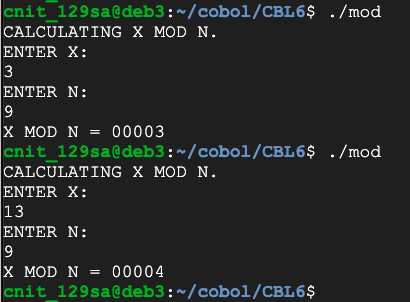
Create a program that will perform modular arithmetic, as shown below.

Hint: the DIVIDE verb can output the remainder.

Flag CBL 6.2: Modulus (10 pts)

Calculate 1959 mod 42. That's the flag.

Multiplication on a Ring

Create a program that will multiply two numbers on a ring, as shown below.

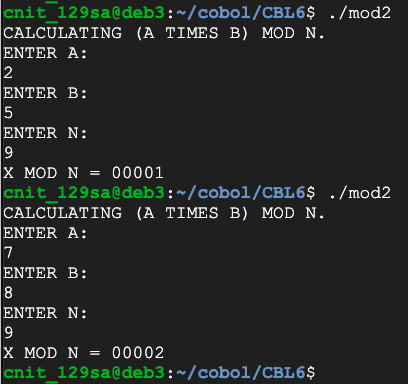
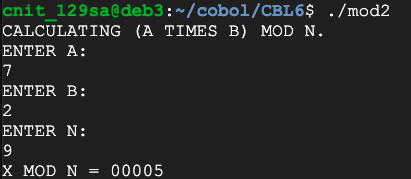
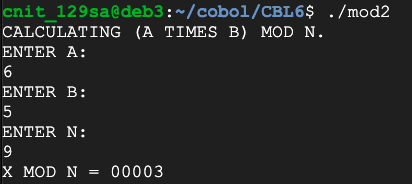
Flag CBL 6.3: Multiplication on a Ring (10 pts)

Calculate 142 times 97 mod 42. That's the flag.

Reversing Multiplication

Suppose I have a message that consists of the numbers 
M = (3, 7, 4, 8)
I want to encrypt them using the ring shown above, with modulus 9, so I multiply them by 2 mod 9, resulting in these values, as shown below: 
M*2 mod 9 = (6, 5, 8, 7)

Multiplicative Inverses

How can I reverse this process? I'd like to divide by two, but there is no such thing as division in modular arithmetic.

However, we can use the "muitiplicative inverse" of 2 mod 9, which is 5.

We encrypted the numbers by multiplying them by 2, and we can decrypt them by multiplying again by 5, as shown below: 

(M*2 mod 9) * 5 mod 9 = (6, 5, 8, 7) * 5 mod 9 = (3, 7, 4, 8)

Why does this work? Because 

(2*5 mod 9) = 1
Therfore, for any number N, 
(2 * N * 5 mod 9) = N * (2 * 5 mod 9) = N * 1 = N

Flag CBL 6.4: Reversing Multiplication on a Ring (10 pts)

I took a secret 4-digit number and encrypted each digit, multiplying it by 2 mod 9. The result was: 
4871
Recover the original 4-digit number. That's the flag.

Finding a Multiplicative Inverse

There are faster methods for finding multiplicative inverses, but we'll use a simple brute-force approach.

This program calculates all possible multiplications: 

IDENTIFICATION DIVISION.  
   PROGRAM-ID. MODINV.  
  
DATA DIVISION.  
   WORKING-STORAGE SECTION.  
      01 WS-A PIC 9(5).
      01 WS-B PIC 9(5).
      01 WS-X PIC 9(5).
      01 WS-N PIC 9(5).
      01 WS-X-MOD-N PIC 9(5).

PROCEDURE DIVISION.  
   DISPLAY "CALCULATING A LOT OF (A TIMES B) MOD N VALUES.".
   DISPLAY "ENTER A:".
   ACCEPT WS-A.
   DISPLAY "ENTER N:".
   ACCEPT WS-N.

   PERFORM VARYING WS-B FROM 1 BY 1 UNTIL WS-B > WS-N
      MULTIPLY WS-A BY WS-B GIVING WS-X
      CALL 'MOD-SUB' USING WS-X, WS-N, WS-X-MOD-N
      DISPLAY WS-A " TIMES " WS-B ' MOD N = ' WS-X-MOD-N
   END-PERFORM.
STOP RUN.
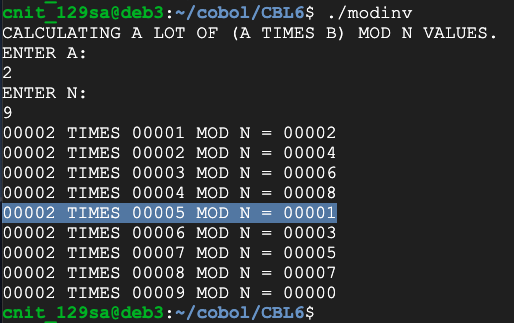
As shown below, you can find the modular inverse by finding the number that results in 1. The multiplicative inverse of 2 mod 9 is 5.

Flag CBL 6.5: Multiplicative Inverse (10 pts)

Find the multiplicative inverse of 13 mod 42. That's the flag.

Flag CBL 6.6: Multiplicative Inverse (10 pts)

Find the multiplicative inverse of 999 mod 1337. That's the flag.

Posted 4-13-2020 by Sam Bowne