At the "Product key" screen, click Cancel.
In the "New Project" window, on the left, expand the "Visual C++" container.
Click Win32.
In the center pane, accept the default selection of "Win32 Console Application".
At the bottom of the "New Project" window, type a Name of YOURNAME-6xa, replacing "YOURNAME" with your own name. Do not use any spaces in the name.
In the "Location" line, click the Browse button and navigate to a folder you have permission to save files in, such as your desktop.
Click the "Select folder" button.
In the "New Project" window, click OK.
A box opens, titled "Welcome to the Win32 Application Wizard".
Click Next. In the next screen, accept the default settings and click Finish.
A window opens, showing a simple C program.
Modify this program to match the code shown in text and the image below.
Do not use the literal string "YOURNAME"--replace it with your own name.
// YOURNAME-6xa.cpp : Defines the entry point for the console application.
//
#include "stdafx.h"
int _tmain(int argc, _TCHAR* argv[])
{
int i=3;
if (i == 3){
printf("YOURNAME-6xa: i is 3\n");
}
else {
printf("YOURNAME-6xa: i is not 3\n");
}
return 0;
}

You should see the message "Build: 1 succeeded" at the bottom of the window. If you see errors, you need to correct them and re-compile the program.
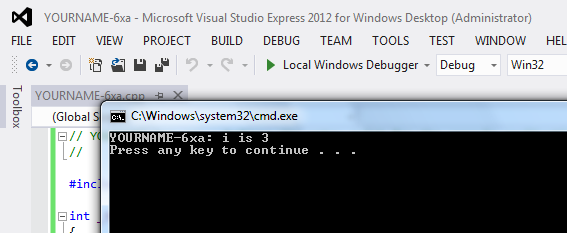
A Command Prompt window opens, showing the output of "YOURNAME-6xa: i is 3", as shown below:
Minimize the Visual Studio Express window.
Start IDA Pro Free.
In the "About" box, click OK.
Agree to the license.
Close the Help window.
In the "Welcome to IDA!" box, click the New button.
In the "New disassembly database" box, double-click "PE Executable".
In the "Select PE Executable to disassemble" box, navigate to the folder you used to save your program in Visual Studio Express, probably your desktop.
Double-click the "YOURNAME-6xa" folder.
Double-click the Debug folder.
Double-click the YOURNAME-6xa.exe file.
In the "PE Executable file loading Wizard", click Next, Next, Finish.
A box appears, saying this file was linked with debug information.
Click Yes
IDA Pro loads the file. As before, the graph mode doesn't show the interesting part of the program.
Expand the Strings. Double-click one of the strings containing "YOURNAME-6xa".
The location containing the string appears.
To the right of "YOURNAME-6xa" there is a "DATA XREF" comment. To the right of the "XREF", double-click "wmain".
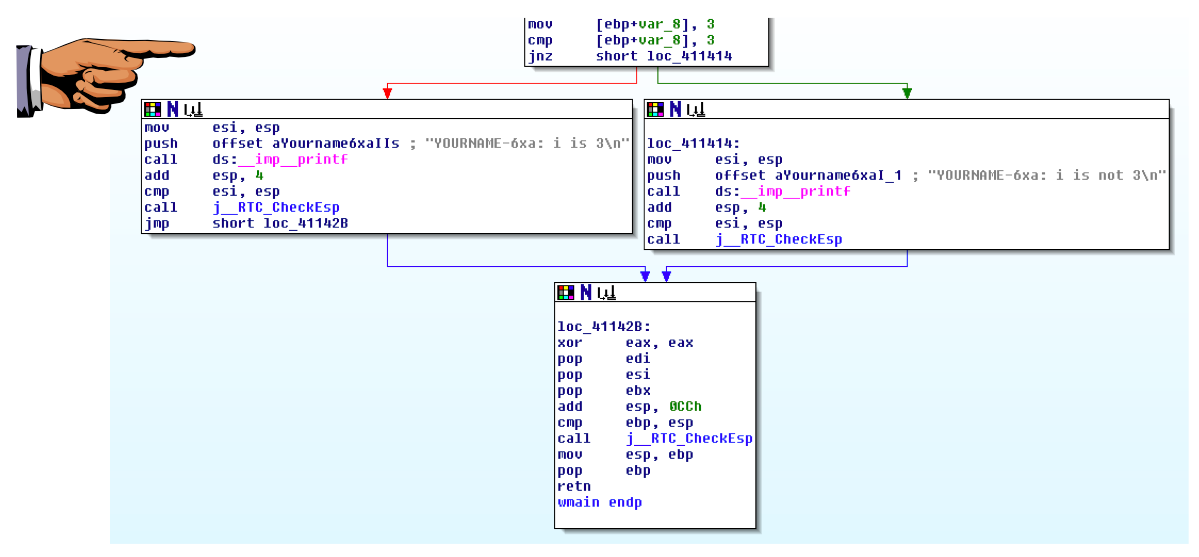
Now the assembly code that performs the task you wrote in C appears, as shown below.
IDA Pro's graph mode makes if statements easy to understand!
The top box ends with a cmp operation (compare two numbers), and a jnz operation (Jump if Not Zero).
The red arrow shows the path taken if the condition is false, and the green arrow shows the path taken if the condition is true.
Click Start, type in PAINT, and open Paint.
Press Ctrl+V to paste in the image of your desktop.
YOU MUST SUBMIT WHOLE-DESKTOP IMAGES TO GET FULL CREDIT.
Save the image with a filename of "Proj 6xa from YOUR NAME".
Print appropriate messages containing your name in all three cases.
Compile it and disassemble it, producing assembly code similar to that shown below.
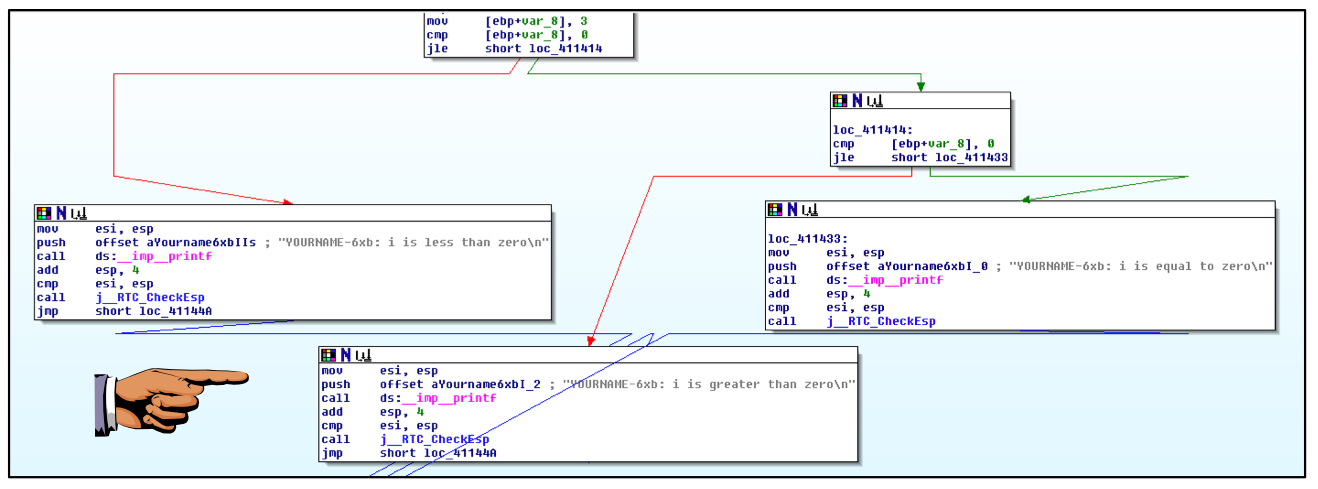
It must show these features:
Last Modified: 9-22-13 2:22 pm